题目内容
1.以△ABC的边BC为弦,在点A的同侧画$\widehat{BC}$交AB于点D,且∠BDC=90°+$\frac{1}{2}$∠A,点P是$\widehat{BC}$上的一个动点.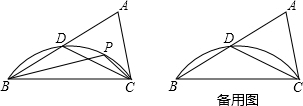
(1)判定△ADC的形状,并说明理由;
(2)若∠A=70°,∠ABC=30°,BP平分∠ABC时,求∠ACB和∠ACP的度数;
(3)是否存在这样位置的P点和AB上一点M,使得△BMP和△BPC相似?若存在,请在备用图中画出所有符合条件的图形(并说明点P和点M的位置);若不存在,请说明理由.
分析 (1)根据三角形的内角和为180°与邻补角的性质,即可求得∠ACD=∠ADC,又由等角对等边,即可求得△ADC是等腰三角形;
(2)利用三角形的内角和定理,可得∠ACB=80°,根据已知即可求得∠BPC=∠BDC=125°,然后可得∠PCB与∠ACP的度数;
(3)由当点P运动至$\widehat{CD}$的中点时,△BMP和△BPC相似,可得∠ABP=∠CBP,即可设∠A=x°,∠ABP=∠CBP=y°,利用方程式可得∠PCB=∠ACP,即可得到∠BMP=∠CNP=90°+$\frac{1}{2}$x°=∠BPC,即可求解.
解答 解:(1)△ADC是等腰三角形.
理由为:∵∠BDC=90°+$\frac{1}{2}$∠A,
∴∠ADC=90°-$\frac{1}{2}$∠A,
∴∠ACD=90°+$\frac{1}{2}$∠A-∠A=90°-$\frac{1}{2}$∠A,
∴∠ACD=∠ADC,
∴△ADC是等腰三角形.
(2)∵∠A=70°,∠PBA=∠PBC=15°,
∴∠ACB=180°-70°-2×15°=80°,
∵∠BPC=∠BDC=90°+$\frac{1}{2}$×70°=125°,
∴∠PCB=180°-15°-125°=40°,
∴∠ACP=∠ACB-∠PCB=80°-40°=40°.
答:∠ACB为80°,∠ACP为40°.
(3)当点P运动至$\widehat{CD}$的中点时,△BMP∽△BPC.
∵P运动至$\widehat{CD}$的中点,
∴∠ABP=∠CBP,
设∠A=x°,∠ABP=∠CBP=y°,
∴∠PCB=180°-y°-(90°+$\frac{1}{2}$x°)=90°-y°-$\frac{1}{2}$x°,
∵∠ACB=180°-x°-2y°,
∴∠ACP=∠ACB-∠PCB=(180°-x°-2y°)-(90°-y°-$\frac{1}{2}$x°)=90°-y°-$\frac{1}{2}$x°,
∴∠PCB=∠ACP,
∴PC平分∠ACB.
∴当点P运动至$\widehat{CD}$的中点时,点P是△ABC的角平分线的交点.
∴AP平分∠BAC.
如图,连接AP,过点P作PM⊥AB交AB于点M,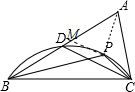
∴∠BMP=∠CNP=90°+$\frac{1}{2}$x°=∠BPC,
∴△BMP∽△BPC.
点评 本题考查了三角形内角和定理,邻补角的性质以及相似三角形的判定与性质.解题的关键是方程思想与数形结合思想的应用.

| A. | (-2,0) | B. | (-1,0) | C. | (2,0) | D. | (5,0) |
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;为了方便顾客,售价定位多少时可获利1200元;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定此时的销售单价,并求出此时的最大利润.
| z(元/个) | 16 | 14 | 12 | 10 |
| y(个) | 120 | 180 | 240 | 300 |
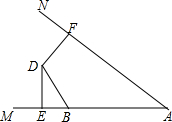 如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由.
如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由. 画出下列各三角形BC边上的高AD.
画出下列各三角形BC边上的高AD. 如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.
如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.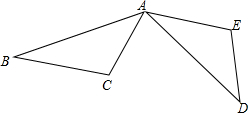 如图,△ABC按逆时针方向旋转得到△ADE
如图,△ABC按逆时针方向旋转得到△ADE