题目内容
18. 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴方程.
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.
(3)在抛物线上BC之间是否存在一点D,使得△DBC的面积最大?若存在请求出点D的坐标和△DBC的面积;若不存在,请说明理由.
分析 (1)直接把点B(8,0)代入抛物线y=-$\frac{1}{4}{x^2}$+bx+4,求出b的值即可得出抛物线的解析式,进而可得出其对称轴方程;
(2)求出A点坐标,再由锐角三角函数的定义得出tan∠ACO=tan∠CBO,故∠ACO=∠CBO,由此可得出结论;
(3)求出BC解析式,将S△BCD转化为$\frac{1}{2}$DH•OB,设D(t,-$\frac{1}{4}$t2+$\frac{3}{2}$t+4),H(t,-$\frac{1}{2}$t+4),面积可转化为S△BCD=-$\frac{1}{8}$(t-4)2+2,△DBC的最大面积为2,此时D点坐标为(4,6).
解答 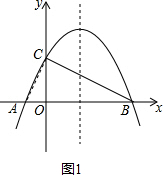 解:(1)∵B点的坐标为B(8,0),
解:(1)∵B点的坐标为B(8,0),
∴-16+8b+4=0,解得b=$\frac{3}{2}$,
∴抛物线的解析式为y═-$\frac{1}{4}{x^2}$+$\frac{3}{2}$x+4,
对称轴方程为x=-$\frac{\frac{3}{2}}{2×(-\frac{1}{4})}$=3;
(2)∵由(1)知,抛物线的对称轴方程为x=3,B(8,0)
∴A(-2,0),C(0,4),
∴OA=2,OC=4,OB=8,
∴tan∠ACO=tan∠CBO=$\frac{1}{2}$,
∴∠ACO=∠CBO.
∵∠AOC=∠COB=90°,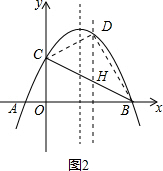
∴△AOC∽△COB.
(3)设BC解析式为y=kx+b,
把(8,0),(0,4)分别代入解析式得,
$\left\{\begin{array}{l}8k+b=0\\ b=4\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=4\end{array}\right.$,
解得y=-$\frac{1}{2}$x+4,
作DH⊥x轴,交BC于H.
设D(t,-$\frac{1}{4}$t2+$\frac{3}{2}$t+4),H(t,-$\frac{1}{2}$t+4),
S△BCD=$\frac{1}{2}$DH•OB=$\frac{1}{2}$×(-$\frac{1}{4}$t2+$\frac{3}{2}$t+4+$\frac{1}{2}$t-4)×8=-$\frac{1}{8}$t2+t=-$\frac{1}{8}$(t2-8t+42-16)=-$\frac{1}{8}$(t-4)2+2,
当t=4时,△DBC的最大面积为2,此时D点坐标为(4,6).
点评 本题考查了二次函数综合题,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案| A. | (-2,0) | B. | (-1,0) | C. | (2,0) | D. | (5,0) |




 如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.
如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.