题目内容
11．在x轴上有两点A（-2，0），B（4，0），如果点C（m，n）在第二象限内，且△ABC的面积为12，求m的取值范围和n的值．分析 先求出AB，根据△ABC的面积为12，得到$\frac{1}{2}×6n=12$，解得：n=4，由点C（m，n）在第二象限内，可得m＜0．
解答 解：∵两点A（-2，0），B（4，0），
∴AB=4-（-2）=6，
∵△ABC的面积为12，
∴$\frac{1}{2}×6n=12$，
解得：n=4，
∵点C（m，n）在第二象限内，
∴m＜0．
点评 本题考查联立坐标与图形的性质，解决本题的关键是表示出△ABC的面积．
练习册系列答案
阅读快车系列答案
相关题目
14．
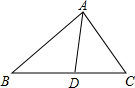如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD=（ ）
如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD=（ ）| A． | 3：4 | B． | 4：3 | C． | 16：9 | D． | 9：16 |
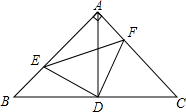如图，在△ABC中，∠A=90°，AB=AC，D 是BC的中点，点E、F分别是AB，AC上的点，并且BE=AF
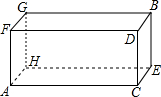有一长方体纸盒，如图所示小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离．若长方体的底面边长AC为12．宽CE为9．高CD为7，请你帮助该小组计算出由A到B的最短路线．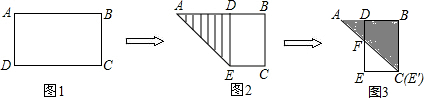
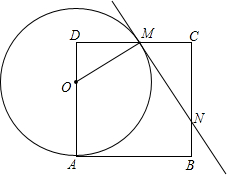如图，在边长为8的正方形ABCD中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点M，连接OM，过点M作⊙O的切线交边BC于N．