Question

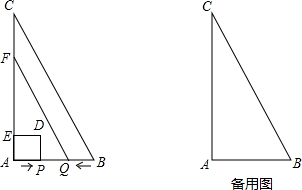
4．如图，在△ABC中，∠A=90°，AB=6cm，AC=8cm．动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停止运动，以AP为一边向上作正方形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为ts，正方形和梯形重合部分的面积为Scm²．
（1）当t=3s时，点P与点Q重合；
（2）当t=$\frac{12}{5}$s时，点D在QF上；
（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式；
（4）是否存在某一时刻，使得正方形APDE的面积被直线QF平分？若存在，直接写出t的值；若不存在，请说明理由．

Answer 1

分析 （1）当点P与点Q重合时，此时AP=BQ=t，且AP+BQ=AB=6，由此列一元一次方程求出t的值；
（2）当点D在QF上时，如答图1所示，此时AP=BQ=t．由相似三角形比例线段关系可得PQ=$\frac{1}{2}$t，从而由关系式AP+PQ+BQ=AB=6，列一元一次方程求出t的值；
（3）当点P在Q，B两点之间（不包括Q，B两点）时，运动过程可以划分为两个阶段：
①当3＜t≤4时，如图3所示，此时重合部分为梯形PDGQ．先计算梯形各边长，然后利用梯形面积公式求出S；
②当4＜t＜6时，如图4所示，此时重合部分为一个多边形．面积S由关系式“S=S_{正方形APDE}-S_△AQF-S_△DMN”求出；
（4）根据当3＜t≤4时，正方形APDE的面积被直线QF平分，求出时间t．

解答 解：（1）当点P与点Q重合时，AP=BQ=t，且AP+BQ=AB=6，
∴t+t=6，解得t=3s，
故答案：3．
（2）当点D在QF上时，如图1所示，此时AP=BQ=t．
∵QF∥BC，APDE为正方形，
∴△PQD∽△ABC，
∴DP：PQ=AC：AB=2，
则PQ=$\frac{1}{2}$DP=$\frac{1}{2}$AP=$\frac{1}{2}$t，
AP+PQ+BQ=AB=6，得t+$\frac{1}{2}$t+t=6，
解得：t=$\frac{12}{5}$．
故答案：$\frac{12}{5}$．
（3）当P、Q重合时，由（1）知，此时t=3，
当D点在BC上时，如图2所示，
AP=BQ=t，BP=$\frac{1}{2}$t，
求得t=4s，
可知此时点E与点F重合，
当点P到达B点时，此时t=6，
因此当P点在Q，B两点之间（不包括Q，B两点）时，其运动过程可分析如下：
①当3＜t≤4时，如图3所示，
此时重合部分为梯形PDGQ．
此时AP=BQ=t，
∴AQ=6-t，PQ=AP-AQ=2t-6，
易知△ABC∽△AQF，
可得AF=2AQ，EF=2EG．
∴EF=AF-AE=2（6-t）-t=12-3t，EG=$\frac{1}{2}$EF=6-$\frac{3}{2}$t，
∴DG=DE-EG=t-（6-$\frac{3}{2}$t）=$\frac{5}{2}$t-6．
S=S_梯形PDGQ=$\frac{1}{2}$（PQ+DG）•PD
=$\frac{1}{2}$[（2t-6）+（$\frac{5}{2}$t-6）]•t，
=$\frac{9}{4}$t²-6t；
②当4＜t＜6时，如图4所示，
重合部分为一个多边形．
AP=BQ=t，
∴AQ=PB=6-t，
易知△ABC∽△AQF∽△PBM∽△DNM，
可得AF=2AQ，PM=2PB，DM=2DN，
∴AF=12-2t，PM=12-2t．
又∵DM=DP-PM=t-（12-2t）=3t-12，
∴DN=$\frac{1}{2}$（3t-12）=$\frac{3}{2}$t-6，
DM=3t-12．
S=S_{正方形APDE}-S_△AQF-S_△DMN=AP²-$\frac{1}{2}$AQ•AF-$\frac{1}{2}$DN•DM
=t²-$\frac{1}{2}$（6-t）（12-2t）-$\frac{1}{2}$×$\frac{1}{2}$（3t-12）×（3t-12）
=-$\frac{9}{4}$t²+30t-72．
（4）由题意得，当3＜t≤4正方形APDE的面积被直线QF平分，
$\frac{9}{4}$t²-6t=$\frac{1}{2}$t²，
解得t=$\frac{24}{7}$．

点评 本题是运动型综合题，涉及到动点与动线问题．第（1）（2）问均涉及动点问题，列方程即可求出t的值；第（3）问涉及动线问题，是本题难点所在，首先要正确分析动线运动过程，然后再正确计算其对应的面积S．本题难度较大，需要同学们具备良好的空间想象能力和较强的逻辑推理能力．