题目内容
14.$\left\{\begin{array}{l}{a-b+c=2}\\{4a+2b+c=17}\\{5a+4b+c=24}\end{array}\right.$.分析 因为三个方程中c的系数相同,应用加减法来解.
解答 解:$\left\{\begin{array}{l}{a-b+c=2①}\\{4a+2b+c=17②}\\{5a+4b+c=24③}\end{array}\right.$,
②-①得:a+b=5④,
③-①得:4a+5b=22⑤,
把④代入⑤得:20-4b+5b=22,
解得:b=2,
把b=2代入④得:a=3,
把a=3,b=2代入①得:c=1,
所以方程组的解是:$\left\{\begin{array}{l}{a=3}\\{b=2}\\{c=1}\end{array}\right.$.
点评 解三元一次方程组要注意以下几点:
方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.

练习册系列答案
相关题目
5.下列说法不正确的是( )
| A. | 等边三角形有三条对称轴 | |
| B. | 线段AB只有一条对称轴 | |
| C. | 等腰三角形的对称轴是底边上的中线 | |
| D. | 等腰三角形的对称轴是底边上的高所在的直线 |
9.某种品牌的八宝粥,外包装标明:净含量为330±10g,表明了这罐八宝粥的净含量x的范围是( )
| A. | 320<x<340 | B. | 320≤x<340 | C. | 320<x≤340 | D. | 320≤x≤340 |
19.在以下实数$\frac{π}{3}$,$\frac{\sqrt{2}}{2}$,1.414,1.010010001…,42,$\frac{1}{6}$中无理数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.计算-x2•2x3的结果是( )
| A. | -2x5 | B. | 2x5 | C. | -2x6 | D. | 2x6 |
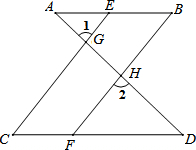 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: 如图,点C在AB的延长线上,CE⊥AF于点E,交BF于点D.若∠F=40°,∠C=20°,则∠FBC的度数为110°.
如图,点C在AB的延长线上,CE⊥AF于点E,交BF于点D.若∠F=40°,∠C=20°,则∠FBC的度数为110°.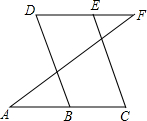 填写理由:如图所示
填写理由:如图所示