题目内容
20．解不等式组：$\left\{\begin{array}{l}{2x＞1-x}\\{x+2＜4x-1}\end{array}\right.$．分析 首先解每个不等式，两个不等式的解集的公共部分就是所求不等式组的解集．
解答 解：$\left\{\begin{array}{l}{2x＞1-x…①}\\{x+2＜4x-1…②}\end{array}\right.$，
解①得：x＞$\frac{1}{3}$，
解②得：x＞1．
则不等式组的解集是：x＞1．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
相关题目
10．当a2+a-1=0时，$\frac{2}{{a}^{2}+a}$-$\frac{a+2}{{a}^{2}+2a+1}$的结果是（ ）
| A． | $\frac{-1-\sqrt{5}}{2}$ | B． | $\frac{-1+\sqrt{5}}{2}$ | C． | 1 | D． | 0 |
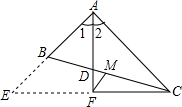在△ABC中，AC＞AB，M为BC的中点．AD是∠BAC的平分线，若CF⊥AD交AD的延长线于F．求证：MF=$\frac{1}{2}$﹙AC-AB﹚．
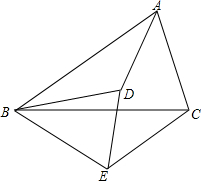已知，如图，$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$，那么△ABD与△BCE相似吗？为什么？
5．下列说法不正确的是（ ）
| A． | 等边三角形有三条对称轴 | |
| B． | 线段AB只有一条对称轴 | |
| C． | 等腰三角形的对称轴是底边上的中线 | |
| D． | 等腰三角形的对称轴是底边上的高所在的直线 |