题目内容
9.某商店经销一种销售成本为每千克40元的水产品,据市场分析,若每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,针对这种水产品情况,请解答以下问题:(1)当销售单价定为每千克55元时,计算销售量和月销售利润.
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的关系式.
(3)销售单价涨多少元时,商场平均每天盈利最多?
分析 (1)根据题意计算即可;
(2)利润=销售量×单位利润.单位利润为x-40,销售量为500-10(x-50),据此表示利润得关系式;(3)设销售单价定为每千克x元,获得利润为w元,则可以根据成本,求出每千克的利润.以及按照销售价每涨1元,月销售量就减少10千克,可求出销量.从而得到总利润关系式,求最值.
解答 解:(1)销售量:500-5×10=450(kg);
销售利润:450×(55-40)=450×15=6750(元);
(2)y=(x-40)[500-10(x-50)]=-10x2+1400x-40000;(3)y=-10x2+1400x-40000=-10(x-70)2+9000,
∴当x=70时,利润最大为9000元.
则涨价为70-50=20(元).
答:应涨价20元时获得的利润最大,最大利润是9000元.
点评 本题主要考查了二次函数的应用,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
相关题目
4.某种型号的国产轿车行驶路程x(千米)和耗油y(升)可以表示为y=$\frac{2}{25}$x.
(1)根据上述关系式填写如表:
(2)分别写出这个问题中的自变量和因变量.
(1)根据上述关系式填写如表:
| 行驶路程x/千米 | 80 | 120 | 140 | 200 |
| 耗油量y/升 | $\frac{32}{5}$ | $\frac{48}{5}$ | $\frac{56}{5}$ | 16 |
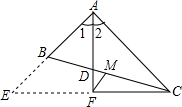 在△ABC中,AC>AB,M为BC的中点.AD是∠BAC的平分线,若CF⊥AD交AD的延长线于F.求证:MF=$\frac{1}{2}$﹙AC-AB﹚.
在△ABC中,AC>AB,M为BC的中点.AD是∠BAC的平分线,若CF⊥AD交AD的延长线于F.求证:MF=$\frac{1}{2}$﹙AC-AB﹚.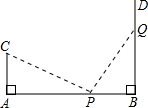 如图,AB=12米,CA⊥AB于A,DB⊥AB于B,且AC=4米,P点从B向A运动,每分钟走1米,Q点从B向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟后,△CAP≌△PBQ?试说明理由.
如图,AB=12米,CA⊥AB于A,DB⊥AB于B,且AC=4米,P点从B向A运动,每分钟走1米,Q点从B向D运动,每分钟走2米,P、Q两点同时出发,运动几分钟后,△CAP≌△PBQ?试说明理由.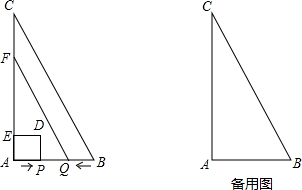
 已知:如图,AC⊥BC,CD∥FG,∠1=∠2,试说明:DE⊥AC.
已知:如图,AC⊥BC,CD∥FG,∠1=∠2,试说明:DE⊥AC.