题目内容
2.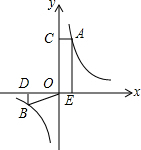 如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.
如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.
分析 根据四边形ACOE的面积为12cm2,可得出反比例函数的解析式y=$\frac{k}{x}$,根据反比例函数y=$\frac{k}{x}$中k的几何意义,可得出△OBD的面积.
解答 解:∵点A、B分别是反比例函数图象上的点,
∴S四边形ACOE=|k|,
∴k=12,
∵S△OBD=$\frac{1}{2}$|k|,
∴S△OBD=6,
故答案为6.
点评 本题考查的是反比例函数系数k的几何意义,即在反比例函数y=$\frac{k}{x}$的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
相关题目
13.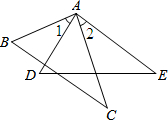 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )| A. | AE=AC | B. | ∠B=∠D | C. | BC=DE | D. | ∠C=∠E |
17.八(1)班组织了一次汉字听写比赛,甲、乙两队各10人,其比赛成绩如下表(10分制):
(1)甲队成绩的中位数是9分,乙队成绩的众数是10分.
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
| 甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
| 乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
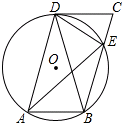 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE. 如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置.
如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置. 已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数.
已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数.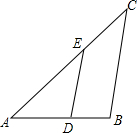 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.