题目内容
17.八(1)班组织了一次汉字听写比赛,甲、乙两队各10人,其比赛成绩如下表(10分制):| 甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
| 乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
分析 (1)利用中位数的定义以及众数的定义分别求出即可;
(2)首先求出平均数进而利用方差公式得出即可;
(3)根据方差的意义即可得出答案.
解答 解:(1)把这组数据从小到大排列7,8,8,9,9,9,10,10,10,10,
甲队成绩的中位数是$\frac{9+9}{2}$=9;
∵在乙队中,10出现了5次,出现的次数最多,
∴乙队成绩的众数是10;
故答案为:9,10;
(2)甲队的平均成绩是:$\frac{1}{10}$(7+8+9+10+10+10+10+9+9+8)=9,
方差是:$\frac{1}{10}$[(7-9)2+2×(8-9)2+3×(9-9)2+4×(10-9)2]=1.
(3)∵乙队成绩的方差是1.4,甲队成绩的方差是1,
∴成绩较为整齐的是甲队.
故答案为:甲.
点评 本题考查了中位数、方差的定义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
8.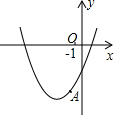 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )| A. | b2>4ac | B. | m>n | ||
| C. | 方程ax2+bx+c=-4的两根为-5或-1 | D. | ax2+bx+c≥-6 |
12.在实数0,π,$\frac{12}{11}$,-$\sqrt{4}$,$\sqrt{3}$中,是无理数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
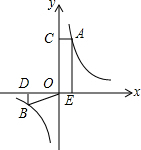 如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.
如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2. 如图,无盖的长方体盒子的长为15,宽为10,高为8,在顶点B处(盒子里面)有一滴蜂蜜,一只蚂蚁在顶点A处,想从盒子的A点爬到盒子的B点,爬行的最短路程是$\sqrt{529}$cm.
如图,无盖的长方体盒子的长为15,宽为10,高为8,在顶点B处(盒子里面)有一滴蜂蜜,一只蚂蚁在顶点A处,想从盒子的A点爬到盒子的B点,爬行的最短路程是$\sqrt{529}$cm.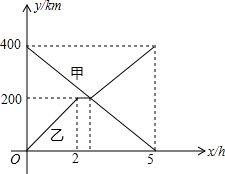 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题: 下面的哪个平面图形绕轴旋转一周得到的几何体从上面看到的如图所示( )
下面的哪个平面图形绕轴旋转一周得到的几何体从上面看到的如图所示( )


