题目内容
12．
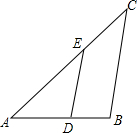如图，已知△ABC∽△ADE，AE=5cm，EC=3cm，BC=7cm，∠BAC=45°，∠C=40°．（1）求∠AED和∠ADE的大小；
（2）求DE的长．
分析 （1）由三角形内角和定理求出∠B=95°，由相似三角形的性质得出∠AED=∠C=40°，∠ADE=∠B=95°即可；
（2）由相似三角形的对应边成比例得出$\frac{AE}{AC}=\frac{DE}{BC}$，即可得出DE的长．
解答 解：（1）∵∠BAC=45°，∠C=40°，
∴∠B=180°-45°-40°=95°，
∵△ABC∽△ADE，
∴∠AED=∠C=40°，∠ADE=∠B=95°；
（2）∵△ABC∽△ADE，
∴$\frac{AE}{AC}=\frac{DE}{BC}$，
即$\frac{5}{5+3}=\frac{DE}{7}$，
解得：DE=$\frac{35}{8}$（cm）．
点评 本题考查了相似三角形的性质、三角形内角和定理；熟练掌握相似三角形的性质是解决问题的关键．
练习册系列答案
相关题目
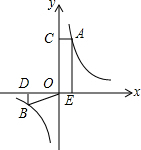如图所示，点A、B分别是反比例函数图象上的点，AE⊥x轴于点E，AC⊥y轴于点C，BD⊥x轴于点D，连接BO，若四边形ACOE的面积为12cm2，则△OBD的面积为6cm2．
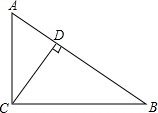如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，tan∠ACD=$\frac{3}{4}$，AB=5，那么CD的长是$\frac{12}{5}$．
下面的哪个平面图形绕轴旋转一周得到的几何体从上面看到的如图所示（ ）
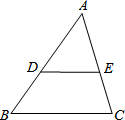如图，在△ABC中，DE∥BC，AD=3cm，BD=2cm，则△ADE与△ABC的相似比为$\frac{3}{5}$．
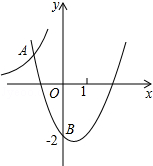如图，二次函数y=x2+bx+c的图象过点B（0，-2）．它与反比例函数y=-$\frac{12}{x}$的图象交于点A（m，4），求这个二次函数的解析式．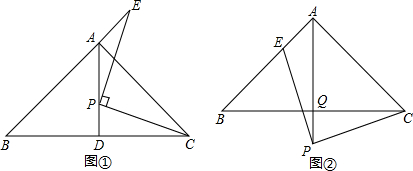
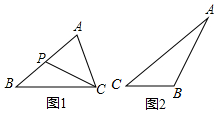王华在学习相似三角形时，在北京市义务教育教科书九年级上册第31页遇到这样一道题，如图1，在△ABC中，P是边AB上的一点，连接CP，要使△ACP∽△ABC，还需要补充的一个条件是∠ACP=∠B（或∠APC=∠ACB），或AC2=AP•AB．