题目内容
10.已知圆的两条平行的弦长分别为6cm和8cm,圆的半径为5cm,则两条平行弦的距离为7cm或1cm.分析 过O点作OE⊥AB于E,交CD于F点,连OA、OC,根据垂径定理和勾股定理分别求出OE、OF的长,根据当圆心O在AB与CD之间时,AB与CD的距离=OE+OF;当圆心O不在AB与CD之间时,AB与CD的距离=OE-OF计算即可.
解答 解:如图,AB∥CD,AB=6cm,CD=8cm,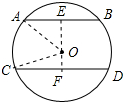
过O点作OE⊥AB于E,交CD于F点,连OA、OC,
∴AE=BE=$\frac{1}{2}$AB=3,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴CF=FD=$\frac{1}{2}$CD=4,
在Rt△OAE中,OA=5cm
OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=4,
同理可得OF=3,
当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7cm,
当圆心O不在AB与CD之间时,AB与CD的距离=OE-OF=4-3=1cm,
故答案为:7cm或1cm.
点评 本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧,也考查了勾股定理,注意分情况讨论思想的应用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.我们定义一种新运算a&b(a,b是实数),规定:a&b=a2-ab-10b,等式右边是正常的实数运算,若x&2=4,则x的值为( )
| A. | 6或-4 | B. | -6或4 | C. | 1+$\sqrt{41}$或1-$\sqrt{41}$ | D. | 5或-4 |
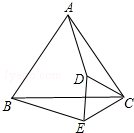 如图所示,已知:△ABC和△CDE都是等边三角形.求证:AD=BE.
如图所示,已知:△ABC和△CDE都是等边三角形.求证:AD=BE.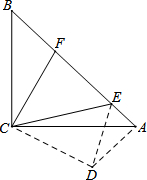 已知,如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是斜边AB上的两点,且∠FCE=45°.
已知,如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是斜边AB上的两点,且∠FCE=45°.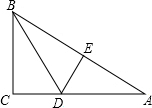 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.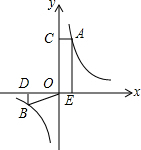 如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.
如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.