题目内容
13.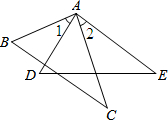 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )| A. | AE=AC | B. | ∠B=∠D | C. | BC=DE | D. | ∠C=∠E |
分析 求出∠BAC=∠DAE,再根据全等三角形的判定定理逐个判断即可.
解答 解:∵∠1=∠2,
∵∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
A、符合SAS定理,即能推出△ABC≌△ADE,故本选项错误;
B、符合ASA定理,即能推出△ABC≌△ADE,故本选项错误;
C、不符合全等三角形的判定定理,即不能推出△ABC≌△ADE,故本选项正确;
D、符合AAS定理,即能推出△ABC≌△ADE,故本选项错误;
故选C.
点评 本题考查了全等三角形的判定定理的应用,能熟练地掌握全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
1.我们定义一种新运算a&b(a,b是实数),规定:a&b=a2-ab-10b,等式右边是正常的实数运算,若x&2=4,则x的值为( )
| A. | 6或-4 | B. | -6或4 | C. | 1+$\sqrt{41}$或1-$\sqrt{41}$ | D. | 5或-4 |
8.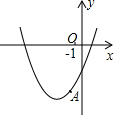 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )| A. | b2>4ac | B. | m>n | ||
| C. | 方程ax2+bx+c=-4的两根为-5或-1 | D. | ax2+bx+c≥-6 |
 已知:如图,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点.
已知:如图,C为线段AB上一点,D为AC的中点,E为BC的中点,F为DE的中点. 已知,如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是斜边AB上的两点,且∠FCE=45°.
已知,如图,在Rt△ABC中,∠ACB=90°,AC=BC,点E、F分别是斜边AB上的两点,且∠FCE=45°.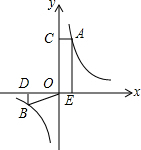 如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.
如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.