题目内容
11.已知?ABCD的顶点B(1,1),C(5,1),直线BD,CD的解析式分别是y=kx,y=mx-14,则BC=4,点A的坐标是(3,7).分析 由顶点B(1,1),C(5,1),即可求得BC的长,又由直线BD,CD的解析式分别是y=kx,y=mx-14,利用待定系数法即可求得k与m的值,继而求得D的坐标,再由四边形ABCD是平行四边形,根据平移的性质,即可求得答案.
解答 解:∵顶点B(1,1),C(5,1),
∴BC=5-1=4;
∵直线BD,CD的解析式分别是y=kx,y=mx-14,
∴1=k,1=5m-14,
解得:k=1,m=3,
∴直线BD,CD的解析式分别是y=x,y=3x-14,
∴$\left\{\begin{array}{l}{y=x}\\{y=3x-14}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=7}\end{array}\right.$,
∴D的坐标为:(7,7),
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴A的坐标为:(3,7).
故答案为:4,(3,7).
点评 此题考查了平行四边形的性质以及一次函数的交点问题.注意掌握平移的性质的应用是解此题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
1.我们定义一种新运算a&b(a,b是实数),规定:a&b=a2-ab-10b,等式右边是正常的实数运算,若x&2=4,则x的值为( )
| A. | 6或-4 | B. | -6或4 | C. | 1+$\sqrt{41}$或1-$\sqrt{41}$ | D. | 5或-4 |
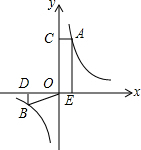 如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.
如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.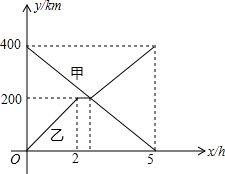 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题: 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )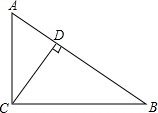 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.