题目内容
16.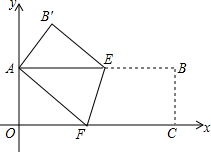 如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.
如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.
分析 过E作EG⊥OC,根据点B的坐标可求出OA=BC=3,OC=AB=9,设OF=x,在Rt△AOF中利用勾股定理可求出OF的长,进而可求出CF的长,可得点F坐标,同理在Rt△AEB′中利用勾股定理可求出AE的长,进而可求出BE的长,得出OG的长,可得点E坐标,证△B'AH∽△AFO,根据对应边成比例得B'H=$\frac{9}{5}$、AH=$\frac{12}{5}$,可得点B'坐标.
解答 解:过E作EG⊥OC,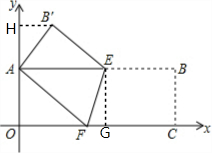
∵点B的坐标为(9,3),
∴OA=BC=3,OC=AB=9,
设OF=x,则AF=CF=9-x,
在Rt△AOF中,AF2=OA2+OF2,即(9-x)2=32+x2,解得x=4,
∴点F坐标为(4,0),
同理,设B′E=x,则AE=9-x,在Rt△AEB′中,
AE2=AB′2+B′E2,即(9-x)2=32+x2,解得x=4,即BE=4,
∴OG=AE=AB-BE=5,
∴E点坐标为(5,3).
过点B'作B'H⊥y轴于点H,
∵∠B'AF=90°,∠B'HA=∠AOF=90°,
∴∠B'AH=∠AFO,
∴△B'AH∽△AFO,
∴$\frac{B'H}{AO}=\frac{AH}{OF}=\frac{AB'}{FA}$,即$\frac{B'H}{3}=\frac{AH}{4}=\frac{3}{5}$,
解得:B'H=$\frac{9}{5}$,AH=$\frac{12}{5}$,
则OH=AO+AH=3+$\frac{12}{5}$=$\frac{27}{5}$,
故点B'的坐标为($\frac{9}{5}$,$\frac{27}{5}$).
点评 本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

 名校课堂系列答案
名校课堂系列答案 如图,己知点A(2,0),直线y=2x+2交x轴于点B,在此直线上找点C,使△ABC为等腰三角形,试求点C的坐标.
如图,己知点A(2,0),直线y=2x+2交x轴于点B,在此直线上找点C,使△ABC为等腰三角形,试求点C的坐标. 如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2016的坐标是(-504,504).
如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2016的坐标是(-504,504).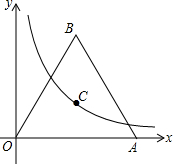 如图,在平面直角坐标系中,双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上的一点C过等边三角形OAB三条高的交点,则点B的坐标为($\sqrt{3}$,$\sqrt{3}$+1).
如图,在平面直角坐标系中,双曲线y=$\frac{\sqrt{3}}{x}$(x>0)上的一点C过等边三角形OAB三条高的交点,则点B的坐标为($\sqrt{3}$,$\sqrt{3}$+1).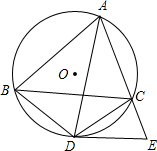 如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.
如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD. 如图是边长为4的正方形,请你建立适当的直角坐标系,并写出点A,B,C,D的坐标.
如图是边长为4的正方形,请你建立适当的直角坐标系,并写出点A,B,C,D的坐标.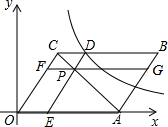 如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )
如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )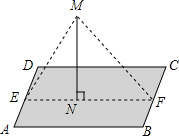 “五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.
“五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.