题目内容
6. 如图,己知点A(2,0),直线y=2x+2交x轴于点B,在此直线上找点C,使△ABC为等腰三角形,试求点C的坐标.
如图,己知点A(2,0),直线y=2x+2交x轴于点B,在此直线上找点C,使△ABC为等腰三角形,试求点C的坐标.
分析 根据直线y=2x+2求得OB=2,由A(2,0),得到OA=2,AB=3,①如图1,当BC=AC时,△ABC为等腰三角形,过C作CD⊥AB,根据等腰三角形的性质得到BD=$\frac{1}{2}$AB=$\frac{3}{2}$,求得OD=$\frac{1}{2}$,于是得到C($\frac{1}{2}$,3);②如图2,当BC=AB=3时,△ABC为等腰三角形,过C作CD⊥AB,根据勾股定理求到C(-1+$\frac{3\sqrt{5}}{5}$,$\frac{6\sqrt{5}}{5}$),③如图2,当AC=AB=3时,△ABC为等腰三角形,根据勾股定理求得C($\frac{1}{5}$,$\frac{12}{5}$).
解答  解:∵直线y=2x+2交x轴于点B,
解:∵直线y=2x+2交x轴于点B,
∴B(-1,0),
∴OB=2,
∵A(2,0),
∴OA=2,∴AB=3,
①如图1,当BC=AC时,△ABC为等腰三角形,
过C作CD⊥AB,
∴BD=$\frac{1}{2}$AB=$\frac{3}{2}$,
∴OD=$\frac{1}{2}$,
∵C在直线y=2x+2上,
∴CD=3,
∴C($\frac{1}{2}$,3);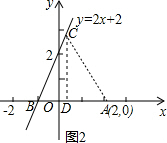
②如图2,当BC=AB=3时,△ABC为等腰三角形,
过C作CD⊥AB,
设OD=x,则CD=2x+2,
∵BD2+CD2=BC2,
∴(1+x)2+(2x+2)2=32,
∴x=-1+$\frac{3\sqrt{5}}{5}$,(负值舍去),
∴C(-1+$\frac{3\sqrt{5}}{5}$,$\frac{6\sqrt{5}}{5}$),
③如图2,当AC=AB=3时,△ABC为等腰三角形,
过C作CD⊥AB,
设OD=x,则CD=2x+2,AD=2-x
∵AD2+CD2=AC2,
∴(2-x)2+(2x+2)2=32,
∴x=$\frac{1}{5}$,(负值舍去),
∴C($\frac{1}{5}$,$\frac{12}{5}$),
综上所述:当△ABC为等腰三角形,点C的坐标为($\frac{1}{2}$,3),(-1+$\frac{3\sqrt{5}}{5}$,$\frac{6\sqrt{5}}{5}$),($\frac{1}{5}$,$\frac{12}{5}$).
点评 本题考查了等腰三角形的判定和性质,一次函数图象上点的坐标特征,勾股定理,分类讨论是解题的关键.

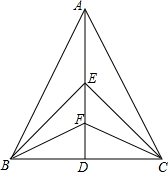 如图,在△ABC中,AB=AC,点E、F是中线AD上的两点,则图中可证明为全等的三角形有( )
如图,在△ABC中,AB=AC,点E、F是中线AD上的两点,则图中可证明为全等的三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |

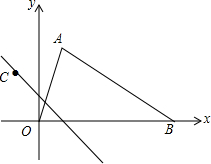 如图,在△AOB中,O是坐标原点,AB=0B,A(1,3),点C在直线y=-x+1上.
如图,在△AOB中,O是坐标原点,AB=0B,A(1,3),点C在直线y=-x+1上.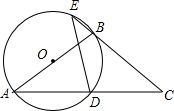 如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.
如图,点D是等腰△ABC底边的中点,过点A、B、D作⊙O.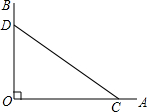 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.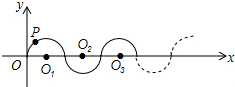 如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1).
如图,在平面直角坐标系中,半径均为1各单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是(2015,-1). 如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.
如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.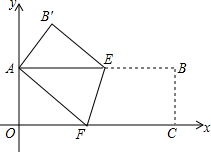 如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.
如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.