题目内容
17．已知一次函数y=kx+b的图象经过点（0，2），且图象与x轴、y轴所围成的三角形的面积为6，求k，b的值．分析 由一次函数图象过点（0，2）可得出b值为2，令y=0，找出点B的坐标，结合三角形的面积公式可得出关于k的方程，解方程即可求出k值．
解答 解：依照题意画出图形，如图所示．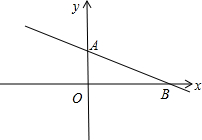
∵一次函数y=kx+b的图象经过点（0，2），
∴2=b，即点A（0，2）．
令y=0，则0=kx+2，解得：x=-$\frac{2}{k}$，
即点B（-$\frac{2}{k}$，0）．
S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×2|-$\frac{2}{k}$|=6，
解得：k=±$\frac{1}{3}$．
∴k=±$\frac{1}{3}$，b=2．
点评 本题考查了一次函数图象上点的坐标特征以及三角形的面积公式，解题的关键是结合三角形面积公式得出关于k的方程．本题属于基础题，难度不大，解决该题型题目时，由点在直线上，可以找出点的坐标，结合三角形面积公式得出关于一次函数系数的方程是关键．
练习册系列答案
相关题目
10．
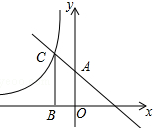如图，直线y=-x+2与y轴交于点A，与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于点C，过点C作CB⊥x轴于点B，AO=2BO，则反比例函数的解析式为（ ）
如图，直线y=-x+2与y轴交于点A，与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于点C，过点C作CB⊥x轴于点B，AO=2BO，则反比例函数的解析式为（ ）| A． | y=$\frac{3}{x}$ | B． | y=-$\frac{3}{x}$ | C． | y=$\frac{3}{2x}$ | D． | y=-$\frac{3}{2x}$ |
如图，已知一次函数y=kx+b的图象与x轴交于点A（5，0），与函数y=2x的图象交于点M，点M的横坐标为2，求点M的坐标及函数y=kx+b的表达式．