题目内容
1.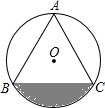 如图,已知边长为6的等边△ABC内接于⊙O.
如图,已知边长为6的等边△ABC内接于⊙O.(1)求⊙O半径;
(2)求$\widehat{BC}$的长和弓形BC的面积.
分析 (1)连结OB,OC,作OM⊥BC于M,根据圆周角定理求出∠BOC的度数,再由锐角三角函数的定义即可得出结论;
(2)直接根据弧长公式可得出弧BC的长,再由弓形BC的面积=S扇形BOC-S△BOC可得出结论.
解答 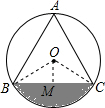 解:(1)连结OB,OC,作OM⊥BC于M,
解:(1)连结OB,OC,作OM⊥BC于M,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠BOC=120°.
又∵OM⊥BC,
∴BM=CM=3.
又∵OB=OC,
∴∠OBC=∠OCB=30°.
∴⊙O半径=$\frac{3}{cos30°}$=2$\sqrt{3}$;
(2)∵由(1)知∠BOC=120°,OB=2$\sqrt{3}$,
∴弧BC的长=$\frac{120π×2\sqrt{3}}{180}$=$\frac{4\sqrt{3}π}{3}$
弓形BC的面积=S扇形BOC-S△BOC=$\frac{120π×(2\sqrt{3})^{2}}{360}$-$\frac{1}{2}$×6×3=4π-3$\sqrt{3}$.
点评 本题考查的是三角形的外接圆与外心,根据题意作出辅助线,利用等边三角形的性质及锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
12.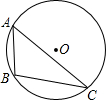 如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
 如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )
如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则$\widehat{BC}$的长为( )| A. | 2π | B. | 4π | C. | 6π | D. | 12π |
16.据统计2015年宁波市实现地区生产总值8011.5亿元,按可比价格计算,比上年增长了8%,把8011.5亿用科学记数法表示是( )
| A. | 8011.5×108 | B. | 801.15×109 | C. | 8.0115×1010 | D. | 8.0115×1011 |
10.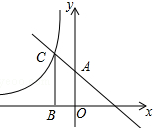 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{3}{2x}$ | D. | y=-$\frac{3}{2x}$ |
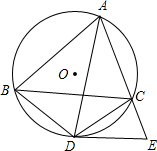 如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.
如图,锐角△ABC内接于⊙O,点D是弧BC上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC,连接AD、BD、CD.