题目内容
18.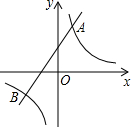 已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)
已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2)(1)求这两个函数的表达式;
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
分析 (1)由A在反比例函数图象上,把A的坐标代入反比例解析式,确定出k的值,从而得出反比例函数解析式,又B也在反比例函数图象上,把B的坐标代入确定出的反比例解析式即可确定出m的值,从而得到B的坐标,由A和B都在一次函数图象上,故把A和B都代入到一次函数解析式中,得到关于a与b的方程组,求出方程组的解得到a与b的值,从而确定出一次函数解析式;
(2)根据图象结合交点坐标即可求得;
(3)由点C与点A关于x轴对称可得AC,AC边上的高为A,B两点横坐标绝对值的和,代入三角形的面积公式即可.
解答 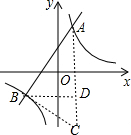 解:(1)∵函数y=$\frac{k}{x}$的图象过点A(1,4),即4=$\frac{k}{1}$,∴k=4,即y1=$\frac{4}{x}$,
解:(1)∵函数y=$\frac{k}{x}$的图象过点A(1,4),即4=$\frac{k}{1}$,∴k=4,即y1=$\frac{4}{x}$,
又∵点B(m,-2)在y1=$\frac{4}{x}$上,
∴m=-2,
∴B(-2,-2),
又∵一次函数y2=ax+b过A、B两点,
即$\left\{\begin{array}{l}{-2a+b=-2}\\{a+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$.
∴y2=2x+2,
综上可得y1=$\frac{4}{x}$,y2=2x+2;
(2)要使y1>y2,即函数y1的图象总在函数y2的图象上方,
∴0<x<1;
(3)过B作BD⊥AC于D,由图形及题意可得:AC=4+4=8,BD=|-2|+1=3,
∴s△ABC=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×8×3=12.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

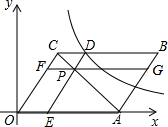 如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )
如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数$y=\frac{k}{x}$的图象经过点D,四边形BCFG的面积为8,则k的值为( )| A. | 16 | B. | 20 | C. | 24 | D. | 28 |
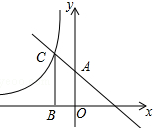 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{3}{2x}$ | D. | y=-$\frac{3}{2x}$ |
