题目内容
5.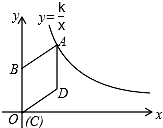 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).(1)求k的值;
(2)将这个菱形沿x轴正方向平移,当顶点D落在反比例函数图象上时,求菱形平移的距离.
分析 (1)根据点D的坐标为(4,3),即可得出DE的长以及DO的长,即可得出A点坐标,进而求出k的值;
(2)根据D′F′的长度即可得出D′点的纵坐标,进而利用反比例函数的性质求出OF′的长,即可得出答案;
解答 解:(1)作DE⊥BO,DF⊥x轴于点F,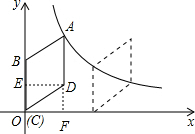 ,
,
∵点D的坐标为(4,3),
∴FO=4,DF=3,
∴DO=5,
∴AD=5,
∴A点坐标为:(4,8),
∴xy=4×8=32,
∴k=32;
(2)∵将菱形ABCD向右平移,使点D落在反比例函数y=$\frac{32}{x}$(x>0)的图象上,
∴DF=3,D′F′=3,
∴D′点的纵坐标为3,
∴3=$\frac{32}{x}$,
x=$\frac{32}{x}$,
∴OF′=$\frac{32}{3}$,
∴FF′=$\frac{32}{3}$-4=$\frac{20}{3}$,
∴菱形ABCD向右平移的距离为:$\frac{20}{3}$.
点评 本题主要考查反比例函数图象上点的坐标特征,利用了菱形的性质,利用了平移的特点,根据已知得出A点坐标是解题关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
16.据统计2015年宁波市实现地区生产总值8011.5亿元,按可比价格计算,比上年增长了8%,把8011.5亿用科学记数法表示是( )
| A. | 8011.5×108 | B. | 801.15×109 | C. | 8.0115×1010 | D. | 8.0115×1011 |
10.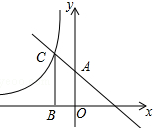 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
 如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )
如图,直线y=-x+2与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=2BO,则反比例函数的解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{3}{2x}$ | D. | y=-$\frac{3}{2x}$ |
 如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017).
如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),$\widehat{A{A}_{1}}$是以点B为圆心,BA为半径的圆弧,$\widehat{{A}_{1}{A}_{2}}$是以点O为圆心,OA1为半径的圆弧,$\widehat{{A}_{2}{A}_{3}}$是以点C为圆心,CA2为半径的圆弧,$\widehat{{A}_{3}{A}_{4}}$是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述做法得到的曲线AA1A2A3A4A5…称为正方形的渐开线“,那么点A5的坐标是(6,0),点A2016的坐标是(1,2017). 在“世界粮食日”前夕,某校团委随机抽取了n名本校学生,对某日午餐剩饭菜情况进行问卷调查.问卷中的剩饭菜情况包括:
在“世界粮食日”前夕,某校团委随机抽取了n名本校学生,对某日午餐剩饭菜情况进行问卷调查.问卷中的剩饭菜情况包括: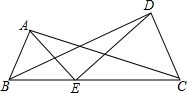 如图,E是线段BC上的一点,A,D是BC同侧的两点,∠AEB=∠DEC,∠ACB=∠BDE,DE=CE,试证明AE=BE.有一位同学是这样思考的:
如图,E是线段BC上的一点,A,D是BC同侧的两点,∠AEB=∠DEC,∠ACB=∠BDE,DE=CE,试证明AE=BE.有一位同学是这样思考的: