题目内容
19.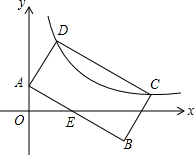 如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为$\frac{3+\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为$\frac{3+\sqrt{5}}{2}$.
分析 证得△AOE≌△BHE≌△DFA≌△BGC,得出BH=BG=DF=OA=1,EH=CG=OE=AF=k-1,即可求得D和C的坐标,然后由反比例函数图象上点的横纵坐标的乘积等于k列出方程组,通过解方程组可以求得k的值.
解答 解:如图,作DF⊥y轴于F,过B点作x轴的平行线与过C点垂直与x轴的直线交于G,CG交x轴于K,作BH⊥x轴于H,
∵四边形ABCD是矩形,
∴∠BAD=90°,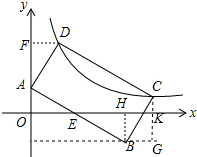
∴∠DAF+∠OAE=90°,
∵∠AEO+∠OAE=90°,
∴∠DAF=∠AEO,
∵AB=2AD,E为AB的中点,
∴AD=AE,
在△ADF和△EAO中,
$\left\{\begin{array}{l}{∠DAF=∠AEO}\\{∠AFD=∠AOE=90°}\\{AD=AE}\end{array}\right.$
∴△ADF≌△EAO(AAS),
∴DF=OA=1,AF=OE,
∴D(1,k),
∴AF=k-1,
同理;△AOE≌△BHE,△ADF≌△CBG,
∴BH=BG=DF=OA=1,EH=CG=OE=AF=k-1,
∴OK=2(k-1)+1=2k-1,CK=k-2
∴C(2k-1,k-2),
∴(2k-1)(k-2)=1•k,
解得k1=$\frac{3+\sqrt{5}}{2}$,k2=$\frac{3-\sqrt{5}}{2}$,
∵k-1>0,
∴k=$\frac{3+\sqrt{5}}{2}$
故答案是:$\frac{3+\sqrt{5}}{2}$.
点评 本题考查了矩形的性质和反比例函数图象上点的坐标特征.图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.在-1,0,2,$\sqrt{3}$四个数中,最大的数是( )
| A. | -1 | B. | 0 | C. | 2 | D. | $\sqrt{3}$ |
10. 如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )
 如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=100°,则∠ACB的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
4.将抛物线y=-x2向左平移1个单位,再向下平移2个单位,所得抛物线的函数关系式是( )
| A. | y=-(x-1)2-2 | B. | y=-(x-1)2+2 | C. | y=-(x+1)2-2 | D. | y=-(x+1)2-2 |
8. 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )| A. | 70° | B. | 40° | C. | 35° | D. | 30° |
 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.当BD=6时,△ABD与△DCE全等.
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.当BD=6时,△ABD与△DCE全等.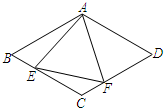 如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=
如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=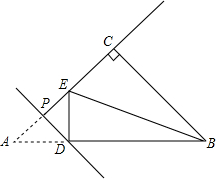 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.
如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.