题目内容
14.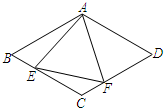 如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=
如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=60°,连接EF,则△AEF的面积最小值是3$\sqrt{3}$.
分析 首先由△ABC是等边三角形,即可得AB=AC,以求得∠ACF=∠B=60°,然后利用平行线与三角形外角的性质,可求得∠AEB=∠AFC,证得△AEB≌△AFC,即可得AE=AF,证得△AEF是等边三角形,当AE⊥BC时得出△AEF的面积最小值即可.
解答 解:当AE⊥BC时,
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
∴∠B=∠ACF=60°,
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,
∠AFC=∠D+∠FAD=60°+∠FAD,
∴∠AEB=∠AFC,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{∠B=∠ACF}\\{∠AEB=∠AFC}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACF(AAS),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∵当AE⊥BC时,AB=4,
∴AE=$2\sqrt{3}$,
∴△AEF的面积最小值=$\frac{1}{2}×\sqrt{3}×\sqrt{3}×2\sqrt{3}=3\sqrt{3}$,
故答案为:$3\sqrt{3}$.
点评 此题考查了菱形的性质,关键是根据等边三角形的判定与性质、全等三角形的判定与性质解答.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
5.江苏省占地面积约为107200平方公里.将107200用科学记数法表示应为( )
| A. | 0.1072×106 | B. | 1.072×105 | C. | 1.072×106 | D. | 10.72×104 |
2.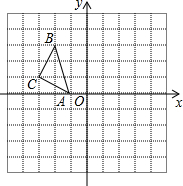 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为( )
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为( )
 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为( )
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,3),C(-3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为( )| A. | (2,1) | B. | (2,3) | C. | (4,1) | D. | (0,2) |
 如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.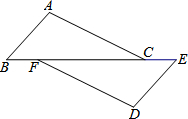 已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.
已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.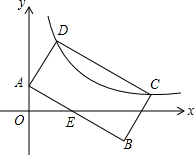 如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为$\frac{3+\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数y=$\frac{k}{x}$(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为$\frac{3+\sqrt{5}}{2}$.