将抛物线y=-x2向左平移1个单位.再向下平移2个单位.所得抛物线的函数关系式是( )A．y=-(x-1)2-2B．y=-(x-1)2+2C．y=-(x+1)2-2D．y=-(x+1)2-2 题目和参考答案——青夏教育精英家教网—

题目内容

4．将抛物线y=-x²向左平移1个单位，再向下平移2个单位，所得抛物线的函数关系式是（　　）

A．

y=-（x-1）²-2

B．

y=-（x-1）²+2

C．

y=-（x+1）²-2

D．

y=-（x+1）²-2

分析易得新抛物线的顶点，根据顶点式及平移前后二次项的系数不变可得新抛物线的解析式．

解答解：原抛物线的顶点为（0，0），向左平移1个单位，再向下平移2个单位，那么新抛物线的顶点为（-1，-2）；
可设新抛物线的解析式为y=-（x-h）²+k代入得：y=-（x+1）²-2．
故选：C．

点评本题考查了二次函数图象与几何变换，抛物线平移不改变二次项的系数的值，解决本题的关键是得到新抛物线的顶点坐标．

练习册系列答案

15．已知扇形的圆心角为60°，半径长为12，则扇形的面积为（　　）

12．函数y=$\frac{1}{{\sqrt{3-x}}}$中，自变量x的取值范围是x＜3．

19．

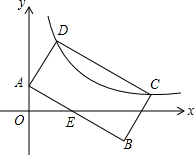如图，矩形ABCD中，AB=2AD，点A（0，1），点C、D在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，AB与x轴的正半轴相交于点E，若E为AB的中点，则k的值为$\frac{3+\sqrt{5}}{2}$．

9．太阳的半径约为696 300km，696 300这个数用科学记数法可表示为（　　）

16．国家统计局4月15日发布的初步测算数据显示，一季度我国社会消费品零售总额为44500亿元，“44500亿元”用科学记数法表示为4.45×10¹²元．

13．计算：
（1）$\frac{y}{4x}$-$\frac{x}{6y}$；（2）$\frac{1}{a-2}$+$\frac{1}{a+2}$；
（3）$\frac{2}{{x}^{2}-2x}$-$\frac{1}{x-2}$；（4）$\frac{2a}{{a}^{2}-9}$-$\frac{2}{3+a}$；
（5）$\frac{1}{a-4}$-$\frac{2}{a+4}$-$\frac{8}{{a}^{2}-16}$；（6）（$\frac{x}{x-2}$-$\frac{x}{x+2}$）÷$\frac{4x}{2-x}$．

14．若方程组$\left\{\begin{array}{l}{2x+3y=m}\\{3x+5y=m+1}\end{array}\right.$的解满足x+y=12，求m的值．

试题分类