题目内容
20．
已知：如图，四边形ABCD中，∠ABC=90°，∠ADC=90°，点E为AC中点，点F为BD中点．求证：EF⊥BD．
分析 连接BE、DE，根据直角三角形斜边上的中线等于斜边的一半可得BE=DE=$\frac{1}{2}$AC，再根据等腰三角形三线合一的性质证明．
解答 
证明：如图，连接BE、DE，
∵∠ABC=90°，∠ADC=90°，点E是AC的中点，
∴BE=DE=$\frac{1}{2}$AC，
∵点F是BD的中点，
∴EF⊥BD．
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形三线合一的性质，熟记性质并作出辅助线是解题的关键．
练习册系列答案
相关题目
12．下面的等式中，y是x的反比例函数的是（ ）
| A． | y=$\frac{1}{{x}^{2}}$ | B． | y=$\frac{1}{2x}$ | C． | y=$\frac{x}{2}$ | D． | y=$\frac{1}{x+2}$ |
在平面直角坐标系中，A（1，2），B（3，1），点P在坐标轴上，S△PAB=4，求P点的坐标．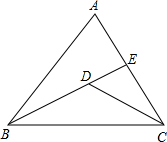
如图，在△ABC中，点D是∠ACB的平分线与∠ABC的平分线的交点，BD的延长线交AC于点E．
如图所示，已知点D、E、F分别是边BC，AC，DC的中点，△EFC的面积为6cm2，则△ABC的面积为48cm2．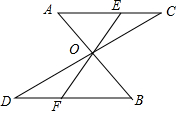
如图AB、CD相交于点O，OA=OB，OC=OD，EF是过O点的任意一条直线，且交AC于点E，交BD于点F，请回答：
10．方程x2-12x+27=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（ ）
| A． | 21 | B． | 21或15 | C． | 15 | D． | 不能确定 |