题目内容
8.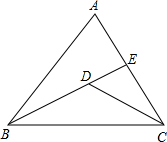 如图,在△ABC中,点D是∠ACB的平分线与∠ABC的平分线的交点,BD的延长线交AC于点E.
如图,在△ABC中,点D是∠ACB的平分线与∠ABC的平分线的交点,BD的延长线交AC于点E.(1)∠AEB、∠EDC、∠DCB的大小关系是∠AEB>∠EDC>∠DCB,理由是三角形的一个外角大于任何一个和它不相邻的内角.
(2)已知∠EDC=60°,求∠A的度数.
分析 (1)根据三角形的一个外角大于任何一个和它不相邻的内角解答;
(2)根据三角形的一个外角大于任何一个和它不相邻的内角计算即可.
解答 解:(1)∵∠AEB是△EBC的外角,
∴∠AEB>∠EDC,
∵∠EDC是△DBC的外角,
∴∠EDC>∠DCB,
∴∠AEB>∠EDC>∠DCB,
故答案为:∠AEB>∠EDC>∠DCB;三角形的一个外角大于任何一个和它不相邻的内角.
(2)∵∠EDC是△CDB的一个外角,
∴∠EDC=∠DCB+∠DBC.
∵∠EDC=60°,
∴∠DCB+∠DBC=60°.
∵DC平分∠ACB,DB平分∠ABC,
∴∠ACB=2∠DCB,∠ABC=2∠DBC,
∴∠ACB+∠ABC=2(∠DCB+∠DBC)=2×600=1200.
∴∠A=180°-(∠ACB+∠ABC)=1800-1200=600.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角大于任何一个和它不相邻的内角是解题的关键.

练习册系列答案
相关题目
20.若关于x的一元二次方程(k-1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<5 | B. | k>5 | C. | k≤5,且k≠1 | D. | k<5,且k≠1 |
1.从九年级一班3名优秀班干部和九二班2名优秀班干部中随机抽取两名学生担任升旗手,则抽取的两名学生刚好一个班的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
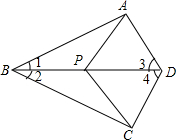 如图,已知∠1=∠2,∠3=∠4,点P是BC上任意一点,求证:PA=PC.
如图,已知∠1=∠2,∠3=∠4,点P是BC上任意一点,求证:PA=PC. 已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD.
已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD. 已知:如图,ED⊥AB,FC⊥AB,垂足分别为D、C,AE‖BF,且AE=BF.求证:AC=BD.
已知:如图,ED⊥AB,FC⊥AB,垂足分别为D、C,AE‖BF,且AE=BF.求证:AC=BD. 如图,已知圆周角∠ACB=130°,则圆心角∠AOB=100°.
如图,已知圆周角∠ACB=130°,则圆心角∠AOB=100°.