题目内容
10．方程x2-12x+27=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（ ）| A． | 21 | B． | 21或15 | C． | 15 | D． | 不能确定 |
分析 先利用因式分解法解方程x2-12x+27=0得到x1=3，x2=9，然后根据三角形三边的关系确定底与腰，再计算三角形的周长．
解答 解：（x-3）（x-9）=0，
x-3=0或x-9=0，
所以x1=3，x2=9，
因为3+3＜9，
所以等腰三角形的底为3，腰为9，
所以三角形的周长为3+9+9=21．
故选A．
点评 本题考查了解一元二次方程-因式分解法：就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了三角形三边的关系．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
已知：如图，四边形ABCD中，∠ABC=90°，∠ADC=90°，点E为AC中点，点F为BD中点．求证：EF⊥BD．
如图，已知圆周角∠ACB=130°，则圆心角∠AOB=100°．
5．下列从左到右的变形，其中是因式分解的是（ ）
| A． | 2（a-b）=2a-2b | B． | x2-2x+1=x（x-2）+1 | ||
| C． | （m+1）（m-1）=m2-1 | D． | 3a（a-1）+（1-a）=（3a-1）（a-1） |
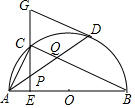如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB于点P、Q，连接AC，给出下列结论：①∠DAC=∠ABC；②AD=CB；③点P是△ACQ的外心；④AC2=AE•AB；⑤CB∥GD，其中正确的结论是（ ）