题目内容
15.已知:3m=2,9n=5,33m-2n+1=$\frac{24}{5}$.分析 逆运用同底数幂相除,底数不变指数相减;同底数幂相乘,底数不变指数相加以及幂的乘方,底数不变指数相乘进行计算即可得解.
解答 解:33m-2n+1=33m÷32n×31,
=(3m)3÷(32)n×3,
=23÷9n×3,
=8÷9×3,
=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 本题考查了同底数幂的除法,同底数幂的乘法,幂的乘方的性质,熟记各性质并熟练应用是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在一个口袋中装有4个完全相同的小球,它们的标号分别为1、2、3、4,从中随机摸出一个小球记下标号放回,再从中随机摸出一个小球,则两次摸出的小球的标号之和大于4的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{8}$ |
5.下列从左到右的变形,其中是因式分解的是( )
| A. | 2(a-b)=2a-2b | B. | x2-2x+1=x(x-2)+1 | ||
| C. | (m+1)(m-1)=m2-1 | D. | 3a(a-1)+(1-a)=(3a-1)(a-1) |
 如图,已知四边形ABCD中∠1=∠2,AB=CD=3,BC=5,求四边形ABCD的周长.
如图,已知四边形ABCD中∠1=∠2,AB=CD=3,BC=5,求四边形ABCD的周长. 已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD.
已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD.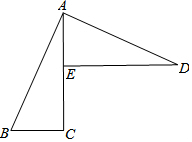 已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.求证:AB=AD.
已知:如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.求证:AB=AD.