题目内容
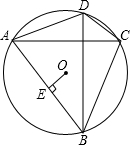 如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E.
如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E.(1)求证:OE=
| 1 |
| 2 |
(2)求证:AB2+CD2=4R2;
(3)若AB、CD是方程x2-6x+4=0的两个根(AB>CD),求⊙O的半径R的值.
考点:圆的综合题
专题:综合题
分析:(1)连结OA、OB、OC、OD,作OF⊥CD于F,如图,根据等腰三角形的性质由OE⊥AB,OF⊥CD得到∠BOE=
∠AOB,∠COF=
∠COD,根据圆周角定理可得∠ACB=
∠AOB,∠CBD=
∠COD,则∠BOE=∠ACB,∠COF=∠CBD,易得∠BOE+∠COF=90°,原式可根据等角的余角相等得到∠COF=∠OBE,然后根据“AAS”证明△BOE≌△OCF,得到OE=CF,再由垂径定理得到CF=DF,所以有OE=
CD;
(2)根据垂径定理得到AE=BE,CF=DF,则AB2+CD2=4BE2+4CF2,由(1)得到CF=OE,则AB2+CD2=4(BE2+4OE2),在Rt△OBE中根据勾股定理得BE2+OE2=R2,于是得到AB2+CD2=4R2;
(3)根据根与系数的关系得到得AB+CD=6,AB•CD=4,则AB2+CD2=(AB+CD)2-2AB•CD=28,再利用(2)的结论AB2+CD2=4R2得4R2=28,然后解方程即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据垂径定理得到AE=BE,CF=DF,则AB2+CD2=4BE2+4CF2,由(1)得到CF=OE,则AB2+CD2=4(BE2+4OE2),在Rt△OBE中根据勾股定理得BE2+OE2=R2,于是得到AB2+CD2=4R2;
(3)根据根与系数的关系得到得AB+CD=6,AB•CD=4,则AB2+CD2=(AB+CD)2-2AB•CD=28,再利用(2)的结论AB2+CD2=4R2得4R2=28,然后解方程即可.
解答:(1)证明:连结OA、OB、OC、OD,作OF⊥CD于F,如图,
∵OE⊥AB,OF⊥CD,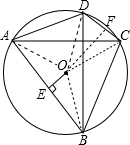
∴∠BOE=
∠AOB,∠COF=
∠COD,
∵∠ACB=
∠AOB,∠CBD=
∠COD,
∴∠BOE=∠ACB,∠COF=∠CBD,
∵AC⊥BD,
∴∠ACB+∠CBD=90°,
∴∠BOE+∠COF=90°,
而∠BOE+∠OBE=90°,
∴∠COF=∠OBE,
在△BOE和△OCF中,
,
∴△BOE≌△OCF(AAS),
∴OE=CF,
而OF⊥CD,
∴CF=DF,
∴OE=
CD;
(2)证明:∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF,
∴AB2+CD2=4BE2+4CF2,
∵CF=OE,
∴AB2+CD2=4BE2+4OE2=4(BE2+4OE2),
在Rt△OBE中,∵BE2+OE2=OB2=R2,
∴AB2+CD2=4R2;
(3)解:根据题意得AB+CD=6,AB•CD=4,
∴AB2+CD2=(AB+CD)2-2AB•CD=62-2•4=28,
∵AB2+CD2=4R2;
∴4R2=28,解得R=
,
即⊙O的半径R的值为
.
∵OE⊥AB,OF⊥CD,

∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOE=∠ACB,∠COF=∠CBD,
∵AC⊥BD,
∴∠ACB+∠CBD=90°,
∴∠BOE+∠COF=90°,
而∠BOE+∠OBE=90°,
∴∠COF=∠OBE,
在△BOE和△OCF中,
|
∴△BOE≌△OCF(AAS),
∴OE=CF,
而OF⊥CD,
∴CF=DF,
∴OE=
| 1 |
| 2 |
(2)证明:∵OE⊥AB,OF⊥CD,
∴AE=BE,CF=DF,
∴AB2+CD2=4BE2+4CF2,
∵CF=OE,
∴AB2+CD2=4BE2+4OE2=4(BE2+4OE2),
在Rt△OBE中,∵BE2+OE2=OB2=R2,
∴AB2+CD2=4R2;
(3)解:根据题意得AB+CD=6,AB•CD=4,
∴AB2+CD2=(AB+CD)2-2AB•CD=62-2•4=28,
∵AB2+CD2=4R2;
∴4R2=28,解得R=
| 7 |
即⊙O的半径R的值为
| 7 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和三角形全等的判定与性质;会运用根与系数的关系和勾股定理进行计算.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知点M(1,a)和点N(2,b)是一次函数y=(k-2)x-3图象上的两点,若a>b,则k的取值范围是( )
| A、k>2 | B、k<0 |
| C、k<2 | D、k≤2 |