题目内容
如图,正方形ABCD的边长为8cm,动点P由点C出发沿折线CB-BA-AD向终点D运动,速度为acm/s;点Q由点B出发,以
cm/s的速度沿对角线BD向终点D运动.两点同时出发,当其中有一个点到达终点时另一个点也停止运动.设运动时间为t(s).
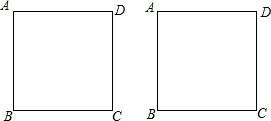
(1)若a=3,求PQ所在直线与BC垂直时t的值;
(2)若a=6,在整个运动过程中,以PQ为直径的圆与直线BD有几次相切,并求出相切时t的值;
(3)是否存在大于2的正数a,使得在整个运动过程中,以PQ为直径的圆与直线BD相切三次?若存在,请直接写出a的值或范围;若不存在,说明理由.
| 2 |

(1)若a=3,求PQ所在直线与BC垂直时t的值;
(2)若a=6,在整个运动过程中,以PQ为直径的圆与直线BD有几次相切,并求出相切时t的值;
(3)是否存在大于2的正数a,使得在整个运动过程中,以PQ为直径的圆与直线BD相切三次?若存在,请直接写出a的值或范围;若不存在,说明理由.
考点:圆的综合题
专题:动点型
分析:(1)分类讨论:P在BC上,P在AD上,根据速度与时间的关系,可得PC、BQ的长,根据勾股定理,可得答案;
(2)分类讨论:P在BC上,P在AD上,P在AB上,运动过程中,已知∠PBQ=45°,直线与圆相切时,PQ⊥BD,围绕等腰直角三角形的两边关系,建立方程求解,可得答案;
(3)分类讨论:P在BC上,P在AD上,P在AB上,根据切线的性质,可得直角三角形,根据勾股定理,可得答案.
(2)分类讨论:P在BC上,P在AD上,P在AB上,运动过程中,已知∠PBQ=45°,直线与圆相切时,PQ⊥BD,围绕等腰直角三角形的两边关系,建立方程求解,可得答案;
(3)分类讨论:P在BC上,P在AD上,P在AB上,根据切线的性质,可得直角三角形,根据勾股定理,可得答案.
解答:解:(1)如图1;
 ,
,
P在BC上时,由题意得PC=3t,BP=8-3t,BQ=
t,
由△BPQ是等腰直角三角形,得
BP=
BP,
即
(8-3t)=
t,
解得t=2;
P在AD上时,PD=8×3-3t,DQ=8
-
t,
由△DPQ是等腰直角三角形,得
DQ=
DP,即
(24-3t)=
(8-t),
解得t=8,
当t=8时,P、Q、D重合,PQ不直线不确定,
综上所述:t=2时,PQ所在直线与BC垂直;
(2)①当P点在BC上时,PQ⊥BD,⊙O与直线BD相切,
由△BQP为等腰直角三角形,得
BQ=PB,即
×
t=8-6t,
解得t1=1,
②当P点在AC上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形,
BQ=PB,即
×
t=6t-8,
解得t2=2,
③当P点在AD上时,PQ⊥BD,⊙O与直线BD相切,
由△DQP为等腰直角三角形,得
DQ=PB,即
(8
-
t)=24-6t,
t3=2(不合题意的要舍去);
综上所述:t=1时,当P点在BC上时,PQ⊥BD,⊙O与直线BD相切;
t=2时,当P点在AC上时,PQ⊥BD,⊙O与直线BD相切;
(3)不存在,由(2)可知,当P点在AD上时,P、Q重合,⊙O不存在,
∴⊙O与直线BD相切只能两次相切,
即t=1时,当P点在BC上时,PQ⊥BD,⊙O与直线BD相切;
t=2时,当P点在AB上时,PQ⊥BD,⊙O与直线BD相切.
 ,
,P在BC上时,由题意得PC=3t,BP=8-3t,BQ=
| 2 |
由△BPQ是等腰直角三角形,得
BP=
| 2 |
即
| 2 |
| 2 |
解得t=2;
P在AD上时,PD=8×3-3t,DQ=8
| 2 |
| 2 |
由△DPQ是等腰直角三角形,得
DQ=
| 2 |
| 2 |
| 2 |
解得t=8,
当t=8时,P、Q、D重合,PQ不直线不确定,
综上所述:t=2时,PQ所在直线与BC垂直;
(2)①当P点在BC上时,PQ⊥BD,⊙O与直线BD相切,
由△BQP为等腰直角三角形,得
| 2 |
| 2 |
| 2 |
解得t1=1,
②当P点在AC上时,PQ⊥BD,⊙O与直线BD相切,
△BQP为等腰直角三角形,
| 2 |
| 2 |
| 2 |
解得t2=2,
③当P点在AD上时,PQ⊥BD,⊙O与直线BD相切,
由△DQP为等腰直角三角形,得
| 2 |
| 2 |
| 2 |
| 2 |
t3=2(不合题意的要舍去);
综上所述:t=1时,当P点在BC上时,PQ⊥BD,⊙O与直线BD相切;
t=2时,当P点在AC上时,PQ⊥BD,⊙O与直线BD相切;
(3)不存在,由(2)可知,当P点在AD上时,P、Q重合,⊙O不存在,
∴⊙O与直线BD相切只能两次相切,
即t=1时,当P点在BC上时,PQ⊥BD,⊙O与直线BD相切;
t=2时,当P点在AB上时,PQ⊥BD,⊙O与直线BD相切.
点评:本题考查了圆的综合题,利用了切线的性质,勾股定理,分类讨论是解题关键,注意不符合题意的要舍去.

练习册系列答案
相关题目
下列语句:①面积相等的两三角形全等;②到线段两端距离相等的点在线段的垂直平分线上;③实数包括有理数和无理数;④点(a2+2,-b2)一定在第四象限.其中正确的语句个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )
如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )A、5
| ||
B、
| ||
C、6-2
| ||
D、
|
下列图形中,不是轴对称图形的是( )
| A、两条相交直线 |
| B、线段 |
| C、有公共端点的两条相等线段 |
| D、有公共端点的两条不相等线段 |
 看图填空:
看图填空: 如图,直线y=
如图,直线y= 如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E.
如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E. 小王为了测量雷州三元塔CD的高度(如图),他先在A处测得塔顶C的仰角为45°,再向塔的方向直行30米到达B处,又测得塔顶C的仰角为60°,请你帮助小王计算出三元塔的高度.(结果精确到1米;参考数据:
小王为了测量雷州三元塔CD的高度(如图),他先在A处测得塔顶C的仰角为45°,再向塔的方向直行30米到达B处,又测得塔顶C的仰角为60°,请你帮助小王计算出三元塔的高度.(结果精确到1米;参考数据: