题目内容
若A(2,O)、B(4,0)是x轴上的两点,点C是y轴上的动点,当∠ACB最大时,则C点的坐标是 .
考点:圆的综合题
专题:压轴题
分析:根据圆周角大于对应的圆外角,当过点A、B的圆与y轴相切于点C时,∠ACB最大(AB的垂直平分线与第一象限的角平分线相交于点P),如图,连结PC,PB,作PH⊥AB,易得OA=2,AB=2,根据垂径定理由PH⊥AB得到AH=BH=1,则OH=OA+AH=3,再与切线的性质得PC⊥OC,可判断四边形PCOH为矩形,得到PC=OH=3,OC=PH,所以PB=PC=3,然后根据勾股定理计算出PH=2
,则有OC=2
,从而可得到C点坐标.
| 2 |
| 2 |
解答:解:过点A、B作圆P,且⊙P与y轴相切于C,如图, 连结PC,PB,作PH⊥AB,
连结PC,PB,作PH⊥AB,
∵A(2,O)、B(4,0),
∴OA=2,AB=2,
∵PH⊥AB,
∴AH=BH=1,
∴OH=OA+AH=3,
∵⊙P与y轴相切于C,
∴PC⊥OC,
∴四边形PCOH为矩形,
∴PC=OH=3,OC=PH,
∴PB=PC=3,
在Rt△PBH中,PH=
=2
,
∴OC=2
,
∴C点坐标为(0,±2
).
故答案为(0,±2
).
 连结PC,PB,作PH⊥AB,
连结PC,PB,作PH⊥AB,∵A(2,O)、B(4,0),
∴OA=2,AB=2,
∵PH⊥AB,
∴AH=BH=1,
∴OH=OA+AH=3,
∵⊙P与y轴相切于C,
∴PC⊥OC,
∴四边形PCOH为矩形,
∴PC=OH=3,OC=PH,
∴PB=PC=3,
在Rt△PBH中,PH=
| PB2-BH2 |
| 2 |
∴OC=2
| 2 |
∴C点坐标为(0,±2
| 2 |
故答案为(0,±2
| 2 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和切线的性质;会运用勾股定理计算线段的长;理解坐标与图形性质.

练习册系列答案
相关题目
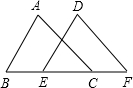 如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF.在下列条件中不能保证△ABC≌△DEF的是( )
如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF.在下列条件中不能保证△ABC≌△DEF的是( )| A、∠B=∠DEF |
| B、AC=DF |
| C、AB∥DE |
| D、∠A=∠D |
 已知二次函数y=2x2
已知二次函数y=2x2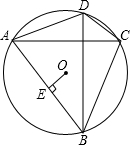 如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E.
如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E. 已知:如图,⊙O中,直径AB⊥弦CD于点E,且CD=24,BE=8,求⊙O的半径.
已知:如图,⊙O中,直径AB⊥弦CD于点E,且CD=24,BE=8,求⊙O的半径.