题目内容
若二次函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是 ．
考点：抛物线与x轴的交点
专题：
分析：m≠0，则函数为二次函数．由抛物线与x轴只有一个交点，得到根的判别式的值等于0，且m不为0，即可求出m的值．
解答：解：∵二次函数y=mx2+2x+1的图象与x轴只有一个公共点，
∴△=4-4m=0，且m≠0，
解得 m=1．
故答案是：1．
∴△=4-4m=0，且m≠0，
解得 m=1．
故答案是：1．
点评：此题考查了一次函数的性质与抛物线与x轴的交点，抛物线与x轴的交点个数由根的判别式的值来确定．本题中函数是二次函数，则二次项系数不等于零．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
32010的个位数字为（ ）
| A、1 | B、3 | C、9 | D、7 |
如图，直线y=
已知二次函数y=2x2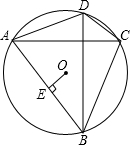
如图，⊙O的半径为R，在⊙O内接四边形ABCD中，AC⊥BD，OE⊥AB于点E．