题目内容
已知△ABC中AB=AC,且BD平分AC,若BD把△ABC的周长分为12cm和15cm两部分,求三边的长.
考点:等腰三角形的性质,三角形三边关系
专题:
分析:由题意可知BD分成的两个三角形的周长的差为△ABC中的腰和底的差,即|AB-BC|=15-12=3cm,再根据腰长相等,设AD=CD=x,则AB=2x,列出方程求出x的值,注意利用三角形的三边关系进行验证.
解答:解:设AD=xcm,则CD=xcm,AB=2xcm,
当△ABD的周长为12cm,△BCD的周长为15cm时,
可知BC-AB=15-12=3cm,此时BC=3+2x,
由题意可知2x+2x+3+2x=12+15,
解得x=4,此时三边长分别为8cm、8cm、11cm,符合三角形三边关系;
当当△ABD的周长为15cm,△BCD的周长为12cm时,
可知AB-BC=15-12=3cm,此时BC=2x-3,
由题意可知2x+2x+2x-3=12+15,
解得x=5,此时三边长分别为10cm、10cm、7cm,符合三角形三边关系;
综上可知三角形的三边长分别为8cm、8cm、11cm或10cm、10cm、7cm.
当△ABD的周长为12cm,△BCD的周长为15cm时,
可知BC-AB=15-12=3cm,此时BC=3+2x,
由题意可知2x+2x+3+2x=12+15,
解得x=4,此时三边长分别为8cm、8cm、11cm,符合三角形三边关系;
当当△ABD的周长为15cm,△BCD的周长为12cm时,
可知AB-BC=15-12=3cm,此时BC=2x-3,
由题意可知2x+2x+2x-3=12+15,
解得x=5,此时三边长分别为10cm、10cm、7cm,符合三角形三边关系;
综上可知三角形的三边长分别为8cm、8cm、11cm或10cm、10cm、7cm.
点评:本题主要考查等腰三角形的性质,分两种情况得出BC和AB的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列语句:①面积相等的两三角形全等;②到线段两端距离相等的点在线段的垂直平分线上;③实数包括有理数和无理数;④点(a2+2,-b2)一定在第四象限.其中正确的语句个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
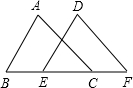 如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF.在下列条件中不能保证△ABC≌△DEF的是( )
如图,已知:在△ABC和△DEF中,如果AB=DE,BC=EF.在下列条件中不能保证△ABC≌△DEF的是( )| A、∠B=∠DEF |
| B、AC=DF |
| C、AB∥DE |
| D、∠A=∠D |
 已知二次函数y=2x2
已知二次函数y=2x2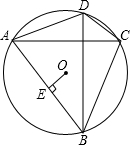 如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E.
如图,⊙O的半径为R,在⊙O内接四边形ABCD中,AC⊥BD,OE⊥AB于点E.