题目内容
7. 如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为4$\sqrt{3}$.
如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为4$\sqrt{3}$.
分析 根据等边三角形的性质可得CD=CB,再根据等边对等角的性质求出∠BDC=∠DBC=30°,然后求出∠BDE=90°,再根据勾股定理列式进行计算即可得解.
解答 解:∵△ABC和△DCE都是边长为4的等边三角形,
∴CB=CD,
∴∠BDC=∠DBC=30°,
又∵∠CDE=60°,
∴∠BDE=90°,
在Rt△BDE中,DE=4,BE=8,
∴BD=$\sqrt{{BE}^{2}-{DE}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了等边三角形的性质,勾股定理的应用,根据题意得出求出△BDE是直角三角形是解题的关键.

练习册系列答案
相关题目
17.向阳村2010年的人均收入为12000元,2012年的人均收入为14520元,求人均收入的年平均增长率.设年平均增长率为x,则根据题意可列方程为( )
| A. | 12000(1-x)2=14520 | B. | 14520(1-x)2=12000 | C. | 12000(1+x)2=14520 | D. | 14520(1+x)2=12000 |
18.若点A(2-a,a+1)在第二象限,则a的取值范围是( )
| A. | a>2 | B. | -1<a<2 | C. | a<-1 | D. | a<1 |
15. 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
 如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )
如图,直线y=-x+m与y=x+3的交点的横坐标为-2,则关于x的不等式-x+m>x+3>0的取值范围为( )| A. | x>-2 | B. | x<-2 | C. | -3<x<-2 | D. | -3<x<-1 |
2.某班学生参加运土劳动,一部分学生抬土,另一部分学生挑土,已知全班共用箩筐99个,扁担66根,求抬土、挑土的学生各有多少人?如果设抬土的同学x人,挑土的同学y人,则可得方程组( )
| A. | $\left\{\begin{array}{l}{2(x+\frac{y}{2})=99}\\{\frac{x}{2}+y=66}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=66}\\{\frac{x}{2}+y=99}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{2}+y=66}\\{\frac{x}{2}+2y=99}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+2y=99}\\{2x+y=66}\end{array}\right.$ |
17.一次函数y=kx-6(k<0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
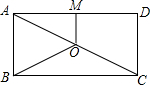 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9. 如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,将△AOD沿着AD翻折,点O恰好落在点E.
如图,正方形ABCD的边长为2,对角线AC、BD相交于点O,将△AOD沿着AD翻折,点O恰好落在点E.