Question

16．如图，正方形ABCD的边长为2，对角线AC、BD相交于点O，将△AOD沿着AD翻折，点O恰好落在点E．
（1）求证：四边形AODE是正方形．
（2）延长CA至点G，使AG=AD，过点G作GF⊥DA的延长线于点F，连结FO，求△DFO的面积．

Answer 1

分析 （1）由正方形的性质可知∠AOD=90°，OA=OD，由翻折的性质可知OA=AE，OD=ED，从而可得到AE=AO=OD=DE，故此可得出要证明的结论；
（2）过点O作OH⊥AD于H．先证明△AFG≌△AOD，从而得到AF=AO=$\sqrt{2}$．，然后依据等腰三角形的性质和直角三角形斜边上的中线的性质可求得OH=1，最后依据三角形的面积公式求解即可．

解答 解：（1）∵四边形ABCD是正方形，
∴OA=OD．
又∵△AOD沿着AD翻折，点O落在点E，
∴AE=AO，DO=DE．
∴AO=DO=DE=AE．
∴四边形AODE是菱形
又∵∠AOD=90°，
∴四边形AODE为正方形．
（2）如图所示：过点O作OH⊥AD于H．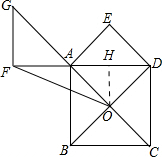

∵在正方形ABCD中，AD=2，∠AOD=90°，
∴AO=DO=$\sqrt{2}$．
∵GF⊥DF，
∴∠GFA=90°
∴∠AOD=∠GFA．
在△AFG和△AOD中$\left\{\begin{array}{l}{∠AOD=∠GFA}\\{∠GAF=∠OAD}\\{AD=AG}\end{array}\right.$
∴△AFG≌△AOD．
∴AF=AO=$\sqrt{2}$．
∵AO=DH，OH⊥AD，
∴H为AD的中点．
∴OH=$\frac{1}{2}$AD=1．
∴S_△FOD=$\frac{1}{2}$FD•OH=$\frac{1}{2}$×（2+$\frac{\sqrt{2}}{2}$）×1=1+$\frac{\sqrt{2}}{2}$．

点评 本题主要考查的是正方形的性质和判定、全等三角形的性质和判定、等腰三角形的性质、直角三角形斜边上中线的性质，证得△AFG≌△AOD是解题的关键．