题目内容
12.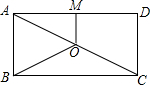 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=3,AD=4,则四边形ABOM的周长为9.
分析 根据题意可知OM是△ADC的中位线,所以OM的长可求;根据勾股定理可求出AC的长,利用直角三角形斜边上的中线等于斜边的一半可求出BO的长,进而求出四边形ABOM的周长.
解答 解:∵O是矩形ABCD的对角线AC的中点,M是AD的中点,
∴OM=$\frac{1}{2}$CD=$\frac{1}{2}$AB=1.5,
∵AB=3,AD=4,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵O是矩形ABCD的对角线AC的中点,
∴BO=$\frac{1}{2}$AC=2.5,
∴四边形ABOM的周长为AB+AM+BO+OM=3+2+2.5+1.5=9,
故答案为:9.
点评 本题考查了矩形的性质、三角形的中位线的性质以及直角三角形斜边上的中线等于斜边的一半这一性质,题目的综合性很好,难度不大.

练习册系列答案
相关题目
2.下列计算中,不正确的是( )
| A. | -2x+3x=x | B. | 2xy2•(-x)=-2x2y2 | C. | (-2x2y)3=-6x2y3 | D. | 6xy2÷2xy=3y |
3.下列各命题的逆命题成立的是( )
| A. | 全等三角形的对应角相等 | |
| B. | 如果两个数相等,那么它们的绝对值相等 | |
| C. | 对角线互相平分的四边形是平行四边形 | |
| D. | 如果两个角都是90°,那么这两个角相等 |
17.若A(2x-5,6-x)在第四象限,则x的取值范围是( )
| A. | x>$\frac{5}{2}$ | B. | x>6 | C. | x$<\frac{5}{2}$ | D. | $\frac{5}{2}<x<6$ |
 如图,?ABCD中,E为BC边上一点,且AB=AE.
如图,?ABCD中,E为BC边上一点,且AB=AE. 如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为4$\sqrt{3}$.
如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为4$\sqrt{3}$. 如图,已知AB∥CD,BC平分∠ABE,∠C=32°,则∠BED的度数是64°.
如图,已知AB∥CD,BC平分∠ABE,∠C=32°,则∠BED的度数是64°.