题目内容
19.解方程组:(1)$\left\{\begin{array}{l}{x-2y=5}\\{3x+y=1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2x+3y=7}\\{4x-5y=3}\end{array}\right.$.
分析 (1)利用加减消元法解出方程组即可;
(2)利用加减消元法解出方程组即可.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=5①}\\{3x+y=1②}\end{array}\right.$,
①+②×2得,7x=7,
解得,x=1,
把x=1代入①得,y=-2,
则方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+3y=7①}\\{4x-5y=3②}\end{array}\right.$,
①×2-②得,11y=11,
解得,y=1,
把y=1代入①得,x=2,
则方程组的解为;$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 本题考查的是二元一次方程组的解法,加减法解二元一次方程组的一般步骤:①方程组的两个方程中,如果同一个未知数的系数既不相等又不互为相反数,就用适当的数去乘方程的两边,使某一个未知数的系数相等或互为相反数.②把两个方程的两边分别相减或相加,消去一个未知数,得到一个一元一次方程.③解这个一元一次方程,求得未知数的值.④将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数的值.⑤把所求得的两个未知数的值写在一起,就得到原方程组的解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知在平面直角坐标系中,点P(a,b)在第四象限,则ab的值不可能为( )
| A. | 5 | B. | -1 | C. | -1.5 | D. | -10 |
 如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为4$\sqrt{3}$.
如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为4$\sqrt{3}$.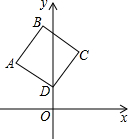 如图,在正方形ABCD中,点D的坐标为(0,1),点A的坐标是(-2,2),则点B的坐标为(-1,4).
如图,在正方形ABCD中,点D的坐标为(0,1),点A的坐标是(-2,2),则点B的坐标为(-1,4). 如图,已知AB∥CD,BC平分∠ABE,∠C=32°,则∠BED的度数是64°.
如图,已知AB∥CD,BC平分∠ABE,∠C=32°,则∠BED的度数是64°. 如图,P是正方形内一点,已知AP=AD,BP=BC,则∠CPD=150°°.
如图,P是正方形内一点,已知AP=AD,BP=BC,则∠CPD=150°°.