题目内容
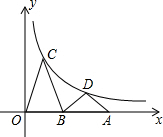 如图,A为x轴上一点,B为OA的中点,C,D为反比例函数y=
如图,A为x轴上一点,B为OA的中点,C,D为反比例函数y=| k |
| x |
考点:反比例函数图象上点的坐标特征,反比例函数系数k的几何意义
专题:计算题
分析:作CE⊥x轴于E点,作DF⊥x轴于F点,如图,根据等腰三角形的性质得OE=BE,BF=AF,由于B点为OA的中点,则OF=3OE,设C(t,
),易得B(2t,0),F(3t,0),A(4t,0),再确定D(3t,
),然后根据三角形面积公式得到
•2t•
+
•2t•
=4,然后解方程即可.
| k |
| t |
| k |
| 3t |
| 1 |
| 2 |
| k |
| t |
| 1 |
| 2 |
| k |
| 3t |
解答:解:作CE⊥x轴于E点,作DF⊥x轴于F点,如图,
 ∵OC=BC,AD=BD,
∵OC=BC,AD=BD,
∴OE=BE,BF=AF,
∵B点为OA的中点,
∴OF=3OE,
设C(t,
),则B(2t,0),F(3t,0),A(4t,0),
当x=3t时,y=
,则D(3t,
),
∵S△OBC+S△ABD=4,
∴
•2t•
+
•2t•
=4,解得k=3.
故答案为3.
 ∵OC=BC,AD=BD,
∵OC=BC,AD=BD,∴OE=BE,BF=AF,
∵B点为OA的中点,
∴OF=3OE,
设C(t,
| k |
| t |
当x=3t时,y=
| k |
| 3t |
| k |
| 3t |
∵S△OBC+S△ABD=4,
∴
| 1 |
| 2 |
| k |
| t |
| 1 |
| 2 |
| k |
| 3t |
故答案为3.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC中,AB=AC,BC=8,其外接圆半径为5,则△ABC的周长为( )
A、8+4
| ||||
B、8+8
| ||||
C、8+4
| ||||
| D、以上都不对 |
在锐角三角形ABC中,BC>AB>AC,小靖依下列方法作图:
(1)作∠A的平分线交BC于D点.
(2)作AD的中垂线交AC于E点.
(3)连接DE.
根据他画的图形,下列关系正确的是( )
(1)作∠A的平分线交BC于D点.
(2)作AD的中垂线交AC于E点.
(3)连接DE.
根据他画的图形,下列关系正确的是( )
| A、DE∥AB |
| B、DE⊥AC |
| C、CD=DE |
| D、CD=BD |
点A(-2,m)与点B(n,4)关于原点对称,则m+n的值是( )
| A、2 | B、6 | C、-2 | D、-6 |
顶点是(-2,1),开口方向,形状与抛物线y=
x2相同的抛物线是( )
| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=-
|

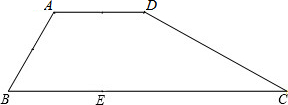
 将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理.
将两个完全相同的长方形拼成如图的图形,长方形的长为a,宽为b,对角线长为c,请你用该图验证勾股定理. 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求证:BA⊥AD.
如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求证:BA⊥AD.