题目内容
 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求证:BA⊥AD.
如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求证:BA⊥AD.考点:勾股定理的逆定理,全等三角形的判定与性质
专题:
分析:延长AD到E,使AD=DE,连接BE,根据SAS推出△ADC≌△EDB,根据全等三角形的性质得出BE=AC=13,求出AB2+AE2=BE2,根据勾股定理的逆定理得出即可.
解答:解: 延长AD到E,使AD=DE,连接BE,
延长AD到E,使AD=DE,连接BE,
∵BC边上的中线AD=6,
∴AE=12,BD=DC,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC=13,
∵AB2+AE2=52+122=169,BE2=132=169,
∴AB2+AE2=BE2,
∴∠BAE=90°,
∴BA⊥AD.
 延长AD到E,使AD=DE,连接BE,
延长AD到E,使AD=DE,连接BE,∵BC边上的中线AD=6,
∴AE=12,BD=DC,
在△ADC和△EDB中,
|
∴△ADC≌△EDB(SAS),
∴BE=AC=13,
∵AB2+AE2=52+122=169,BE2=132=169,
∴AB2+AE2=BE2,
∴∠BAE=90°,
∴BA⊥AD.
点评:本题考查了全等三角形的性质和判定,勾股定理,勾股定理的逆定理的应用,解此题的关键是能正确作出辅助线,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AB=AC,AD=AE,则图中所有全等三角形共有( )
如图,AB=AC,AD=AE,则图中所有全等三角形共有( )| A、3对 | B、4对 | C、5对 | D、6对 |
锐角三角形中,任意两个内角之和必大于( )
| A、120° | B、100° |
| C、90° | D、60° |
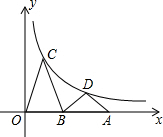 如图,A为x轴上一点,B为OA的中点,C,D为反比例函数y=
如图,A为x轴上一点,B为OA的中点,C,D为反比例函数y=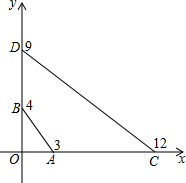 已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由.
已知如图,A,B,C,D四点的坐标分别是(3,0),(0,4),(12,0),(0,9),探索∠OBA和∠OCD的大小关系,并说明理由. 如图,已知⊙O的半径为
如图,已知⊙O的半径为 如图是由五个大小相同的正方体搭成的几何体,从
如图是由五个大小相同的正方体搭成的几何体,从 如图,直线y=-x+4与y轴交于点A,与直线y=0.5x+1交于点B,直线y=0.5x+1与x轴交于点C,求△ABC的面积.
如图,直线y=-x+4与y轴交于点A,与直线y=0.5x+1交于点B,直线y=0.5x+1与x轴交于点C,求△ABC的面积.