题目内容
1.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,实验数据如下表:| 摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)如果实验继续进行下去,根据上表数据,出现“和为6”的频率将稳定在它的概率附近,估计出现“和为6”的概率是0.33.
(2)当x=5时,请用列表法或树状图法计算“和为6”的概率
(3)判断x=5是否符合(1)的结论,若符合,请说明理由,若不符合,请你写出一个符合(1)的x的值.
分析 (1)根据实验次数越大越接近实际概率求出出现“和为6”的概率即可;
(2)根据小球分别标有数字2、3、4、x,用列表法或画树状图法说明当x=5时,得出数字之和为6的概率,即可得出答案;
(3)根据(1)(2)的结果可得出结论.
解答 解:(1)利用图表得出:实验次数越大越接近实际概率,所以出现“和为6”的概率是0.33;
(2)当x=5时,如图,
共有12种情况,和是6的情况共2种,“和为6”的概率=$\frac{2}{12}$=$\frac{1}{6}$;
(3)由(2)可知x=5是不符合(1)的结论,当x=2,3,4时均符合.
点评 此题主要考查了利用频率估计概率,以及列树状图法求概率,注意甲、乙两人每次同时从袋中各随机摸出1个球,列出树状图是解决问题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
11.同时含有字母a,b,c,系数为1的6次单项式按以下规则排序:先看a的次数,a的次数高的单项式排在前面,若相同,再比较b的次数,最后比较c的次数,均是先高次后低次,则a2b3c排在第几位( )
| A. | 第4位 | B. | 第5位 | C. | 第6位 | D. | 第7位 |
12.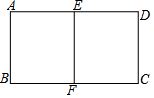 如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
 如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )
如图,在矩形ABCD中,E,F分别为,AD与BC的中点,且矩形ABCD∽矩形AEFB,$\frac{AD}{AB}$的值为( )| A. | 2 | B. | $\frac{5}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
9.可以用来说明命题“若|a|>1,则a>1”是假命题的反例是( )
| A. | a=3 | B. | a=2 | C. | a=-2 | D. | a=-1 |
 如图,在△ABC中,∠ACB=90°,AC=BC=4,D为BC的中点,DE⊥AB,垂足为E.过点B作BF∥AC交DE的延长线于点F,连接CF,AF.现有如下结论:
如图,在△ABC中,∠ACB=90°,AC=BC=4,D为BC的中点,DE⊥AB,垂足为E.过点B作BF∥AC交DE的延长线于点F,连接CF,AF.现有如下结论: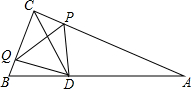 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分线交于点D,动点P,Q从点C同时出发,点P以1cm/s的速度沿射线CA方向运动,点Q以2cm/s的速度沿射线CB方向运动,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s),连接PQ,PD,QD.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=3cm,∠ABC的平分线交于点D,动点P,Q从点C同时出发,点P以1cm/s的速度沿射线CA方向运动,点Q以2cm/s的速度沿射线CB方向运动,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s),连接PQ,PD,QD. 已知直线y=kx+b经过点A(5,0),B(1,4).
已知直线y=kx+b经过点A(5,0),B(1,4).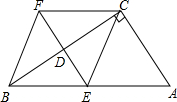 如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE
如图所示,在四边形ABFC,∠ACB=90°,BC垂直平分线EF交BC于点D,交AB于点E,且CF=AE