��Ŀ����
13��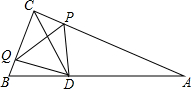 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=6cm��BC=3cm����ABC��ƽ���߽��ڵ�D������P��Q�ӵ�Cͬʱ��������P��1cm/s���ٶ�������CA�����˶�����Q��2cm/s���ٶ�������CB�����˶�������P�����Aʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt��s��������PQ��PD��QD��
��ͼ����Rt��ABC�У���ACB=90�㣬AC=6cm��BC=3cm����ABC��ƽ���߽��ڵ�D������P��Q�ӵ�Cͬʱ��������P��1cm/s���ٶ�������CA�����˶�����Q��2cm/s���ٶ�������CB�����˶�������P�����Aʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt��s��������PQ��PD��QD����1�����ú�t�Ĵ���ʽ��ʾ�߶�PQ�ij���
��2�����D��AC�ľ��룻
��3�����PQD���ABC���ص�����ͼ�ε����ΪS��cm2����
�ٵ�0��t��3ʱ����S��t֮��ĺ�����ϵʽ��
��ֱ��д�����˶�������S��t�����������ʱt��ȡֵ��
���� ��1��������PC=t��QC=2t����Rt��PQC�У�����PQ=$\sqrt{P{C}^{2}+C{Q}^{2}}$�����ɽ�����⣮
��2����ͼ1�У���DE��AC��E��DF��BC��F������֤���ı���CFDE�������Σ��������εı߳�Ϊx����DE��BC���ɵ�$\frac{DE}{BC}$=$\frac{AE}{AC}$����$\frac{x}{3}$=$\frac{6-x}{6}$���ⷽ�̼��ɽ�����⣮
��3������ͼ2�У���MH��AC��M��MG��BC��G�����ı���CGMH�������Σ���߳�Ϊy������������a����0��t��1.5ʱ���ص������ǡ�PQD��b����1.5��t��3ʱ���ص������ǡ�PKD���ֱ���⼴�ɣ�
�ڷ������������ۼ��ɣ�a����0��t��1.5ʱ���ص������ǡ�PQD��b����1.5��t��3ʱ���ص������ǡ�PKD���ֱ���⼴�ɣ�c����t��3ʱ���ֱ����ö��κ��������ʼ��ɽ�����⣮
��� �⣺��1��������PC=t��QC=2t��
��Rt��PQC��PQ=$\sqrt{P{C}^{2}+C{Q}^{2}}$=$\sqrt{{t}^{2}+��2t��^{2}}$=$\sqrt{5}$t��
��2����ͼ1�У���DE��AC��E��DF��BC��F��
�ߡ�ACB=90�㣬DCƽ�֡�ACB��
���DCE=��DCF=��DCE=��CDF=45�㣬
��EC=ED��FC=FD��
��DF��BC��DE��AC��
��DE=DF��
��DE=DF=CF=EC��
���ı���CFDE�����Σ���ECF=90�㣬
���ı���CFDE�������Σ��������εı߳�Ϊx��
��DE��BC��
��$\frac{DE}{BC}$=$\frac{AE}{AC}$��
��$\frac{x}{3}$=$\frac{6-x}{6}$��
��x=2��
���D��AC�ľ���Ϊ2��
��3������ͼ2�У���MH��AC��M��MG��BC��G�����ı���CGMH�������Σ���߳�Ϊy��
��MH��CQ��
��$\frac{MH}{CQ}$=$\frac{PH}{PC}$��
��$\frac{y}{2t}$=$\frac{t-y}{t}$��
��y=$\frac{2}{3}$t��
��0��t��1.5ʱ���ص������ǡ�PQD��
��S=��S��CQD-S��CQM��+��S��CPD-S��CPM��=$\frac{1}{2}$•2t��2-$\frac{2}{3}$t��+$\frac{1}{2}$•t•��2-$\frac{2}{3}$t��=$\frac{3}{2}$t��2-$\frac{2}{3}$t��=3t-t2��
��ͼ3�У���PT��AB��BC��T��QR��AB��R��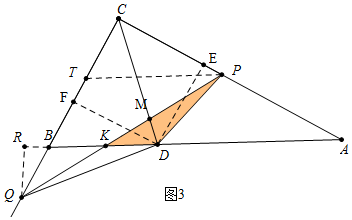
��$\frac{PT}{AB}$=$\frac{PC}{AC}$=$\frac{CT}{BC}$��
��$\frac{PT}{3\sqrt{5}}$=$\frac{t}{6}$=$\frac{CT}{3}$��
��PT=$\frac{\sqrt{5}}{2}$t��CT=$\frac{1}{2}$t��
��BK��PT��
��$\frac{BK}{PT}$=$\frac{QB}{QT}$��
��$\frac{BK}{\frac{\sqrt{5}}{2}t}$=$\frac{2t-3}{2t-\frac{1}{2}t}$��
��BK=$\frac{\sqrt{5}}{3}$��2t-3����
����K���D�غ�ʱ��$\frac{\sqrt{5}}{3}$��2t-3��=$\sqrt{5}$�����t=3��
��KD=$\sqrt{5}$-$\frac{\sqrt{5}}{3}$��2t-3��=2$\sqrt{5}$-$\frac{2}{3}$$\sqrt{5}$t��
�ɡ�QRB�ס�DFB���ɵ�$\frac{QR}{DF}$=$\frac{BQ}{DB}$��
��$\frac{QR}{2}$=$\frac{2t-3}{\sqrt{5}}$��
��QR=$\frac{2\sqrt{5}}{5}$��2t-3����
�൱1.5��t��3ʱ���ص������ǡ�PKD��
S=S��PDQ-S��QDK=3t-t2-$\frac{1}{2}$•��2$\sqrt{5}$-$\frac{2}{3}$$\sqrt{5}$t��•$\frac{2\sqrt{5}}{5}$��2t-3��=$\frac{1}{3}$t2-3t+6��
����������S=$\left\{\begin{array}{l}{3t-{t}^{2}}&{��0��t��1.5��}\\{\frac{1}{3}{t}^{2}-3t+6}&{��1.5��t��3��}\end{array}\right.$��
���ɢٿ�֪����0��t��1.5ʱ��S��t�����������
��ͼ4�У�
��t��3ʱ���ص������ǡ�PDK��S=$\frac{1}{2}$•DK•PH=$\frac{1}{2}$•[$\frac{\sqrt{5}}{3}$��2t-3��-$\sqrt{5}$]•$\frac{\sqrt{5}}{5}$��6-t��=-$\frac{1}{3}$t2+3t-6��
��-$\frac{1}{3}$��0���������£��Գ���t=$\frac{9}{2}$��
��3��t��$\frac{9}{2}$ʱ��S��t�����������
��������������0��t��1.5��3��t��$\frac{9}{2}$ʱ��S��t�����������
���� ���⿼���������ۺ��⡢�����ε��ж������ʡ����ɶ�����ƽ���߷��߶γɱ������������κ�����Ӧ�õ�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ���÷������۵�˼��˼�����⣬ѧ�ṹ�����κ��������ö��κ��������ʽ�����������⣬�����п�ѹ���⣮

| A�� | $\frac{m}{sin��}$ | B�� | mcos�� | C�� | msin�� | D�� | $\frac{m}{cos��}$ |
| �����ܴ��� | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| ����Ϊ6�����ֵ�Ƶ�� | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| ����Ϊ6�����ֵ�Ƶ�� | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
��1�����ʵ�����������ȥ�������ϱ����ݣ����֡���Ϊ6����Ƶ�ʽ��ȶ������ĸ��ʸ��������Ƴ��֡���Ϊ6���ĸ�����0.33��
��2����x=5ʱ�������б�������״ͼ�����㡰��Ϊ6���ĸ���
��3���ж�x=5�Ƿ���ϣ�1���Ľ��ۣ������ϣ���˵�����ɣ��������ϣ�����д��һ�����ϣ�1����x��ֵ��
| A�� | 120.7��109 | B�� | 12.07��1010 | C�� | 1.207��1011 | D�� | 0.1207��1012 |
| A�� | 6.37��106�� | B�� | 6.37��107�� | C�� | 0.637��107�� | D�� | 63.7��105�� |

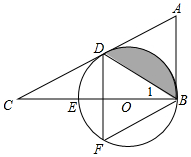 ��ͼ���ڡ�ABC�У���ABC=90�㣬D��AC����һ�㣬����BD��ʹ��A=2��1��E��BC�ϵ�һ�㣬��BEΪֱ���ġ�O������D����F�ڻ�DEB�ϣ�
��ͼ���ڡ�ABC�У���ABC=90�㣬D��AC����һ�㣬����BD��ʹ��A=2��1��E��BC�ϵ�һ�㣬��BEΪֱ���ġ�O������D����F�ڻ�DEB�ϣ�