题目内容
12．
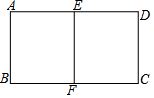如图，在矩形ABCD中，E，F分别为，AD与BC的中点，且矩形ABCD∽矩形AEFB，$\frac{AD}{AB}$的值为（ ）| A． | 2 | B． | $\frac{5}{3}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
分析 根据相似多边形对应边的比相等，设出原来矩形的长与宽，就可得到一个方程，解方程即可求得．
解答 解：∵矩形ABCD∽矩形AEFB，
∴$\frac{AD}{AB}$=$\frac{AB}{AE}$．
设AD=x，AB=y，则AE=$\frac{1}{2}$x．
∴$\frac{x}{y}$=$\frac{y}{\frac{1}{2}x}$，
故y2=$\frac{1}{2}$x2，即x2=2y2，
则x=$\sqrt{2}$y，
则$\frac{AD}{AB}$=$\frac{x}{y}$=$\sqrt{2}$．
故选C．
点评 此题考查了相似多边形的性质，根据相似形的对应边的比相等，把几何问题转化为方程问题，正确分清对应边，以及正确解方程是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．下列各组数不可能是一个三角形的边长的是（ ）
| A． | 5，5，5 | B． | 5，7，7 | C． | 5，12，13 | D． | 5，7，12 |
如图，已知线段AB=a，延长BA至点C，使AC=$\frac{1}{2}$AB．点D为线段BC的中点．
17．
如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（ ）
如图，已知∠1=∠2，则不一定能使△ABD≌△ACD的条件是（ ）| A． | BD=CD | B． | AB=AC | C． | ∠B=∠C | D． | ∠BDA=∠CDA |
4．己知在Rt△ABC中，∠C=90°，∠A=α，BC=m，那么AB的长为（ ）
| A． | $\frac{m}{sinα}$ | B． | mcosα | C． | msinα | D． | $\frac{m}{cosα}$ |
1．一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字2，3，4，x，甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复试验，实验数据如下表：
解答下列问题：
（1）如果实验继续进行下去，根据上表数据，出现“和为6”的频率将稳定在它的概率附近，估计出现“和为6”的概率是0.33．
（2）当x=5时，请用列表法或树状图法计算“和为6”的概率
（3）判断x=5是否符合（1）的结论，若符合，请说明理由，若不符合，请你写出一个符合（1）的x的值．
| 摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
（1）如果实验继续进行下去，根据上表数据，出现“和为6”的频率将稳定在它的概率附近，估计出现“和为6”的概率是0.33．
（2）当x=5时，请用列表法或树状图法计算“和为6”的概率
（3）判断x=5是否符合（1）的结论，若符合，请说明理由，若不符合，请你写出一个符合（1）的x的值．
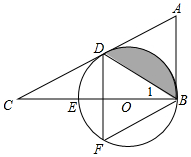如图，在△ABC中，∠ABC=90°，D是AC边上一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D，点F在弧DEB上．