题目内容
10. 已知直线y=kx+b经过点A(5,0),B(1,4).
已知直线y=kx+b经过点A(5,0),B(1,4).(1)求直线AB的函数表达式;
(2)若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4≤kx+b的解集.
分析 (1)利用待定系数法即可求得函数的解析式;
(2)解两个函数解析式组成方程组即可求解;
(3)关于x的不等式2x-4≤kx+b的解集就是函数y=kx+b的图象在上边的部分自变量的取值范围.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{5k+b=0}\\{k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
则直线AB的解析式是y=-x+5;
(2)根据题意得$\left\{\begin{array}{l}{y=-x+5}\\{y=2x-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$,
则C的坐标是(3,2);
(3)根据图象可得不等式的解集是x≤3.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
20.下列各组数不可能是一个三角形的边长的是( )
| A. | 5,5,5 | B. | 5,7,7 | C. | 5,12,13 | D. | 5,7,12 |
1.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,实验数据如下表:
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为6”的频率将稳定在它的概率附近,估计出现“和为6”的概率是0.33.
(2)当x=5时,请用列表法或树状图法计算“和为6”的概率
(3)判断x=5是否符合(1)的结论,若符合,请说明理由,若不符合,请你写出一个符合(1)的x的值.
| 摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)如果实验继续进行下去,根据上表数据,出现“和为6”的频率将稳定在它的概率附近,估计出现“和为6”的概率是0.33.
(2)当x=5时,请用列表法或树状图法计算“和为6”的概率
(3)判断x=5是否符合(1)的结论,若符合,请说明理由,若不符合,请你写出一个符合(1)的x的值.
18.阿里巴巴数据显示,2016年天猫商城“双11”全球狂欢交易额超1207亿元,数据1207亿元用科学记数法表示为( )
| A. | 120.7×109 | B. | 12.07×1010 | C. | 1.207×1011 | D. | 0.1207×1012 |
5.地球赤道的半径为6370000米,用科学记数法表示为( )
| A. | 6.37×106米 | B. | 6.37×107米 | C. | 0.637×107米 | D. | 63.7×105米 |
19.计算(6an+2-9an+1+3an-1)÷3an-1的结果是( )
| A. | 2a3-3a2 | B. | 2a3-3a2+1 | C. | 3a3-6a2+1 | D. | 以上都不对 |
9.王老伯在集市上先买回5只羊,平均每只a元,稍后又买回3只羊,平均每只b元,后来他以每只$\frac{a+b}{2}$的价格把羊全部卖掉了,结果发现赔了钱,赔钱的原因是( )
| A. | a>b | B. | a<b | ||
| C. | a=b | D. | 与a、b的大小关系无关 |
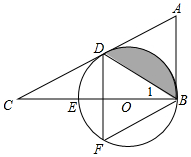 如图,在△ABC中,∠ABC=90°,D是AC边上一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D,点F在弧DEB上.
如图,在△ABC中,∠ABC=90°,D是AC边上一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D,点F在弧DEB上.