题目内容
5.一艘轮船往返甲、乙两港之间,第一次往返航行时,水流速度为a千米/时,第二次往返航行时,正遇上发大水,水流速度为b千米/时(b>a),已知该船在两次航行中的静水速度相同,则该船这两次往返航行所用时间的关系是( )| A. | 第一次往返航行用的时间少 | B. | 第二次往返航行用的时间少 | ||
| C. | 两种情况所用时间相等 | D. | 以上均有可能 |
分析 甲乙两港之间的路程一定,可设其为S,两次航行中的静水速度设为v,所用时间=顺流时间+逆流时间,注意顺流速度=静水速度+水流速度;逆流速度=静水速度-水流速度,把相关数值代入,比较即可.
解答 解:设两次航行的路程都为S,静水速度设为v,
第一次所用时间为:$\frac{S}{v+a}$+$\frac{S}{v-a}$=$\frac{2vS}{{v}^{2}{-a}^{2}}$
第二次所用时间为:$\frac{S}{v+b}$+$\frac{S}{v-b}$=$\frac{2vS}{{v}^{2}{-b}^{2}}$
∵b>a,∴b2>a2,
∴v2-b2<v2-a2
∴$\frac{2vS}{{v}^{2}{-b}^{2}}$>$\frac{2vS}{{v}^{2}{-a}^{2}}$
∴第一次的时间要短些.
故选A.
点评 本题主要考查了列代数式,得到两次所用时间的等量关系是解决本题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
14.某人下午6点到7点之间外出购物,出发和回来时发现表上的时针和分针的夹角都为110°,此人外出购物共用了( )分钟.
| A. | 16 | B. | 20 | C. | 32 | D. | 40 |
10. 如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
 如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )| A. | 80° | B. | 45° | C. | 60° | D. | 70° |
14. 如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
 如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2014 | B. | ($\frac{1}{2}$)2014 | C. | ($\frac{\sqrt{2}}{2}$)2015 | D. | ($\frac{1}{2}$)2015 |
 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图: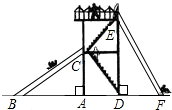 如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.
如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.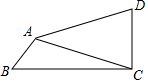 如图,在四边形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,则AC=$\frac{8\sqrt{10}}{5}$.
如图,在四边形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,则AC=$\frac{8\sqrt{10}}{5}$.