题目内容
16. 如图,在△ABC中,按以下步骤作图:
如图,在△ABC中,按以下步骤作图:①以点B为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,以点C为圆心,同样长为半径作弧,两弧分别相交于点M,N;
②作直线MN分别交AB、BC于点D、E,连接CD.
则直线MN和BC的关系是直线MN垂直平分BC.若CD=CA,∠A=50°,求∠ACB的度数.
分析 利用基本作图可判断直线MN垂直平分BC,利用CA=CD得到∠CDA=∠A=50°,则∠ACD=80°,再根据线段垂直平分线的性质得到DB=DC,则∠B=∠DCB,然后利用三角形外角性质得到可计算出∠DCB=25°,于是得到∠ACB=105°.
解答 解:直线MN垂直平分BC.
∵CA=CD,
∴∠CDA=∠A=50°,
∴∠ACD=80°,
∵直线MN垂直平分BC,
∴DB=DC,
∴∠B=∠DCB,
而∠CDA=∠B+∠DCB=50°,
∴∠DCB=25°,
∴∠ACB=80°+25°=105°.
故答案为直线MN垂直平分BC.
点评 本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
5.一艘轮船往返甲、乙两港之间,第一次往返航行时,水流速度为a千米/时,第二次往返航行时,正遇上发大水,水流速度为b千米/时(b>a),已知该船在两次航行中的静水速度相同,则该船这两次往返航行所用时间的关系是( )
| A. | 第一次往返航行用的时间少 | B. | 第二次往返航行用的时间少 | ||
| C. | 两种情况所用时间相等 | D. | 以上均有可能 |
 如图,若不增加字母与辅助线,要得到△ABC∽△ADE,只需要再添加一个条件是DE∥BC(答案不唯一).
如图,若不增加字母与辅助线,要得到△ABC∽△ADE,只需要再添加一个条件是DE∥BC(答案不唯一).
 如图,在△ABC中,点A1、A2是AB的三等分点,点B1、B2是BC的三等分点,点C1、C2、C3、C4是AC的五等分点,记四边形A1A2C3C4、B1B2C1C2的面积分别为S1、S2,若S1+S2=12,则五边形A2BB1C2C3的面积为14.
如图,在△ABC中,点A1、A2是AB的三等分点,点B1、B2是BC的三等分点,点C1、C2、C3、C4是AC的五等分点,记四边形A1A2C3C4、B1B2C1C2的面积分别为S1、S2,若S1+S2=12,则五边形A2BB1C2C3的面积为14.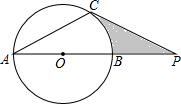 如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,过点C作⊙O的切线交AB的延长线于点P.
如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,过点C作⊙O的切线交AB的延长线于点P.