题目内容
14．某人下午6点到7点之间外出购物，出发和回来时发现表上的时针和分针的夹角都为110°，此人外出购物共用了（ ）分钟．| A． | 16 | B． | 20 | C． | 32 | D． | 40 |
分析 这是一个追及问题，分针走一分走了6度，即分针的角速度是：6度/分，时针一分走0.5度，即角速度是：0.5度/分；由于开始时分针在时针后面110度，后来是分针在时针前面110度，依此列出方程求解即可．
解答 解：设此人外出购物共用了x分钟，则
（6-0.5）x=110+110
5.5x=220
x=40．
答：此人外出购物共用了40分钟．
故选：D．
点评 本题考查钟表时针与分针的夹角．本题关键是根据两个时刻的夹角找到等量关系建立方程求解．
练习册系列答案
相关题目
4．在Rt△OAB中，∠OAB=15°，OC为斜边上的高，且OC=1，P，Q分别为△AOC和△BOC的内心（内心为三角形三条角平分线的交点），连接PQ并延长交OB于M，则OM=（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
如图，若不增加字母与辅助线，要得到△ABC∽△ADE，只需要再添加一个条件是DE∥BC（答案不唯一）．
9．下列四个数中最小的数是（ ）
| A． | -2 | B． | 0 | C． | -$\frac{1}{3}$ | D． | 5 |
19．
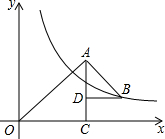如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC-S△BAD为（ ）
如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC-S△BAD为（ ）| A． | 3 | B． | 6 | C． | 12 | D． | 36 |
5．一艘轮船往返甲、乙两港之间，第一次往返航行时，水流速度为a千米/时，第二次往返航行时，正遇上发大水，水流速度为b千米/时（b＞a），已知该船在两次航行中的静水速度相同，则该船这两次往返航行所用时间的关系是（ ）
| A． | 第一次往返航行用的时间少 | B． | 第二次往返航行用的时间少 | ||
| C． | 两种情况所用时间相等 | D． | 以上均有可能 |