题目内容
20.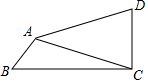 如图,在四边形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,则AC=$\frac{8\sqrt{10}}{5}$.
如图,在四边形ABCD中,∠BCD=90°,∠D+2∠B=180°,AD=5,AB=2,CD=3,则AC=$\frac{8\sqrt{10}}{5}$.
分析 延长BA,CD交于E,作∠ADE的平分线DF交AE于F,过A作AH⊥CD于H,于是得到∠ADE+∠ADC=180°,∠ADE=2∠ADF=2∠EDF,根据已知条件得到∠B=∠EDF,推出∠EFD=90°,根据等腰三角形的性质得到DE=AD=5,根据相似三角形的性质得到EF=4(负值舍去),根据勾股定理得到BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=6,根据相似三角形的性质的AH=$\frac{24}{5}$,EH=$\frac{32}{5}$,由勾股定理即刻得到结论.
解答  解:延长BA,CD交于E,作∠ADE的平分线DF交AE于F,过A作AH⊥CD于H,
解:延长BA,CD交于E,作∠ADE的平分线DF交AE于F,过A作AH⊥CD于H,
则∠ADE+∠ADC=180°,∠ADE=2∠ADF=2∠EDF,
∵∠ADC+2∠B=180°,
∴∠B=∠EDF,
∵∠BCD=90°,
∴∠B+∠E=90°,
∴∠FDE+∠E=90°,
∴∠EFD=90°,
∴DF⊥AE,
∴DE=AD=5,
∵∠E=∠E,
∴△DEF∽△AEC,
∴$\frac{DE}{BE}$=$\frac{EF}{CE}$,即$\frac{5}{2+2EF}$=$\frac{EF}{8}$,
∴EF=4(负值舍去),
∴BE=10,
∴BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=6,
∵AH∥BC,
∴△AEH∽△BEC,
∴$\frac{AE}{BE}$=$\frac{EH}{CE}$=$\frac{AH}{BC}$,
∴AH=$\frac{24}{5}$,EH=$\frac{32}{5}$,
∴CH=$\frac{8}{5}$,
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\frac{8\sqrt{10}}{5}$,
故答案为:$\frac{8\sqrt{10}}{5}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | -2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | 5 |
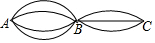 如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )
如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )| A. | 3种 | B. | 4种 | C. | 7种 | D. | 12种 |
| A. | 第一次往返航行用的时间少 | B. | 第二次往返航行用的时间少 | ||
| C. | 两种情况所用时间相等 | D. | 以上均有可能 |
| 运输工具 | 平均速度(千米/小时) | 运费(元/千米) | 装卸总费用(元) |
| 火车 | 120 | 20 | 2400 |
| 汽车 | 100 | 25 | 1600 |
(2)如果汽车运输总费用比火车运输总费用多1600,求A县与B市之间的路程为多少?
(3)如果小李想将这批水果运往C市销售,选择哪种运输工具比较合算?请说明你的理由.
