题目内容
10．
如图，△ABC中，若∠B=∠C，BD=CE，CD=BF，∠A=40°，则∠EDF=（ ）| A． | 80° | B． | 45° | C． | 60° | D． | 70° |
分析 根据题意得出∠B=∠C=70°，再证明△BDF≌△CED，从而得出∠BFD=∠CDE，则∠EDF=∠B．
解答 解：∵AB=AC，∠A=40°，
∴∠B=∠C=70°．
在△BDF与△CED中，$\left\{\begin{array}{l}{BD=CE}&{\;}\\{∠B=∠C}&{\;}\\{BF=CD}&{\;}\end{array}\right.$，
∴△BDF≌△CED（SAS），
∴∠BFD=∠CDE，
∵∠BDF+∠BFD=110°，
∴∠BDF+∠CDE=110°，
∴∠EDF=∠B=70°．
故选B．
点评 本题考查了全等三角形的判定和性质、等腰三角形的性质，三角形内角和定理；证明三角形全等是解决问题的关键．
练习册系列答案
相关题目
19．
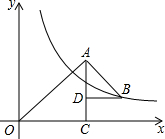如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC-S△BAD为（ ）
如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B，则△OAC与△BAD的面积之差S△OAC-S△BAD为（ ）| A． | 3 | B． | 6 | C． | 12 | D． | 36 |
如图，在△ABC中，点A1、A2是AB的三等分点，点B1、B2是BC的三等分点，点C1、C2、C3、C4是AC的五等分点，记四边形A1A2C3C4、B1B2C1C2的面积分别为S1、S2，若S1+S2=12，则五边形A2BB1C2C3的面积为14．
18．有下列说法：
①由许多条线段连接而成的图形叫做多边形；
②多边形的边数是不小于4的自然数；
③从一个多边形（边数为n）的同一个顶点出发，分别连接这个顶点与其余与之不相邻的各顶点，可以把这个多边形分割成（n-2）个三角形；
④半圆是扇形．
其中正确的结论有（ ）
①由许多条线段连接而成的图形叫做多边形；
②多边形的边数是不小于4的自然数；
③从一个多边形（边数为n）的同一个顶点出发，分别连接这个顶点与其余与之不相邻的各顶点，可以把这个多边形分割成（n-2）个三角形；
④半圆是扇形．
其中正确的结论有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
5．一艘轮船往返甲、乙两港之间，第一次往返航行时，水流速度为a千米/时，第二次往返航行时，正遇上发大水，水流速度为b千米/时（b＞a），已知该船在两次航行中的静水速度相同，则该船这两次往返航行所用时间的关系是（ ）
| A． | 第一次往返航行用的时间少 | B． | 第二次往返航行用的时间少 | ||
| C． | 两种情况所用时间相等 | D． | 以上均有可能 |
如图，在四边形ABCD中，CD=CB，∠B=∠D=90°，∠BAC=55°，则∠ACD的度数为35°．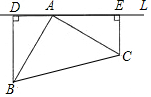
如图，Rt△ABC中，∠BAC=90°，AB=AC，BD⊥直线L于D，CE⊥直线L于E，若BD=5cm，CE=4cm，则DE=9cm．