题目内容
16.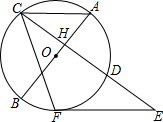 如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.
如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.
分析 连接DF,连接AF交CE于G,由AB是⊙O的直径,且经过弦CD的中点H,得到$\widehat{AC}=\widehat{AD}$,由于EF是⊙O的切线,推出∠GFE=∠GFD+∠DFE=∠ACF=65°根据外角的性质和圆周角定理得到∠EFG=∠EGF=65°,于是得到结果.
解答 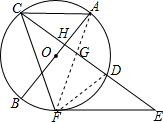 解:连接DF,连接AF交CE于G,
解:连接DF,连接AF交CE于G,
∵AB是⊙O的直径,且经过弦CD的中点H,
∴$\widehat{AC}=\widehat{AD}$,
∵EF是⊙O的切线,
∴∠GFE=∠GFD+∠DFE=∠ACF=65°,
∵∠FGD=∠FCD+∠CFA,
∵∠DFE=∠DCF,
∠GFD=∠AFC,
∠EFG=∠EGF=65°,
∴∠E=180°-∠EFG-∠EGF=50°,
故答案为:50°.
方法二: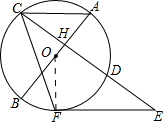
连接OF,易知OF⊥EF,OH⊥EH,故E,F,O,H四点共圆,又∠AOF=2∠ACF=130°,故∠E=180°-130°=50°
点评 本题考查了切线的性质,圆周角定理,垂径定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
6.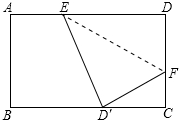 如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
 如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )
如图将矩形ABCD纸片沿EF折叠,使D点与BC边的中点D′重合,若BC=8,CD=6,则CF=( )| A. | $\frac{5}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
4.下列四个几何体:
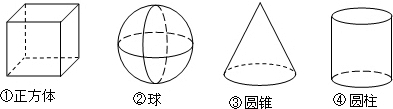
其中左视图与俯视图相同的几何体共有( )

其中左视图与俯视图相同的几何体共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.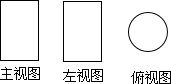 如图是一个几何体的三视图,则该几何体的展开图可以是( )
如图是一个几何体的三视图,则该几何体的展开图可以是( )
 如图是一个几何体的三视图,则该几何体的展开图可以是( )
如图是一个几何体的三视图,则该几何体的展开图可以是( )| A. | 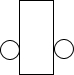 | B. | 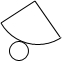 | C. | 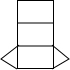 | D. | 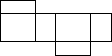 |
6. 如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
 如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:$\sqrt{3}$ |
 如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )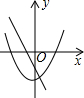
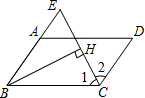 在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.
在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.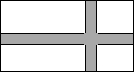 如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.
如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.