题目内容
7. 如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A. | 4 | B. | 5 | C. | 6 | D. | 10 |
分析 如图,首先运用翻折变换的性质证明BE=AE=$\frac{1}{2}$AB;其次运用勾股定理求出AB的长度,即可解决问题.
解答  解:如图,由翻折变换的性质得:
解:如图,由翻折变换的性质得:
BE=AE=$\frac{1}{2}$AB;
∵△ABC为直角三角形,且AC=6,BC=8,
∴AB2=62+82,
∴AB=10,BE=5,
故选B.
点评 该题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;牢固掌握翻折变换的性质、勾股定理等几何知识点是灵活运用、解题的基础和关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
19.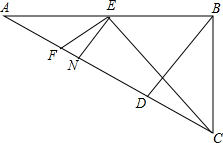 如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
 如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )
如图,在△ABC中,∠ABC=90°,AB=6,BC=4,BD⊥AC于点D,E是AB的中点,连接CE,交BD于点M,点F在AC上,连接EF,过点E作EN∥BD,交AC于点N.若∠FEC=90°,则$\frac{EM}{EF}$的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |
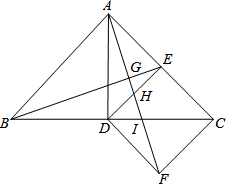 如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.
如图所示,△ABC中,AB=AC,∠BAC=90°,AD⊥BC,DE⊥AC,△CDE沿直线BC翻折到△CDF,连结AF交BE、DE、DC分别于点G、H、I.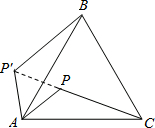 如图所示,P是等边三角形ABC内的一点,且PA=18,PB=24,PC=30.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为18,∠APB=150°.
如图所示,P是等边三角形ABC内的一点,且PA=18,PB=24,PC=30.若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与P′之间的距离为18,∠APB=150°.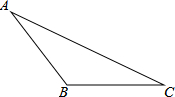 如图,在△ABC中画出高线AD、中线BE、角平分线CF.
如图,在△ABC中画出高线AD、中线BE、角平分线CF.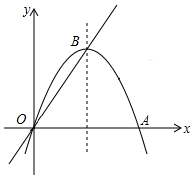 如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.
如图,经过原点O的抛物线y=ax2-6ax交x轴于点A,顶点B在正比例函数y=$\frac{4}{3}$x的图象上.若点M在直线OB上,点N在抛物线的对称轴上,求ON+MN的最小值.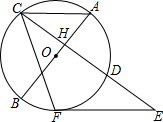 如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.
如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.