题目内容
6. 如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABCD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:$\sqrt{3}$ |
分析 首先设设AC,BD相较于点O,由菱形ABCD的周长为8cm,可求得AB=BC=2cm,又由高AE长为$\sqrt{3}$cm,利用勾股定理即可求得BE的长,继而可得AE是BC的垂直平分线,则可求得AC的长,继而求得BD的长,则可求得答案.
解答 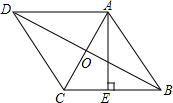 解:如图,设AC,BD相较于点O,
解:如图,设AC,BD相较于点O,
∵菱形ABCD的周长为8cm,
∴AB=BC=2cm,
∵高AE长为$\sqrt{3}$cm,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=1(cm),
∴CE=BE=1cm,
∴AC=AB=2cm,
∵OA=1cm,AC⊥BD,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$(cm),
∴BD=2OB=2$\sqrt{3}$cm,
∴AC:BD=1:$\sqrt{3}$.
故选D.
点评 此题考查了菱形的性质以及勾股定理.注意菱形的四条边都相等,对角线互相平分且垂直.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.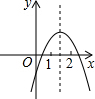 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )
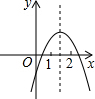 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
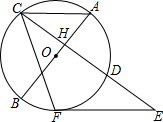 如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.
如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.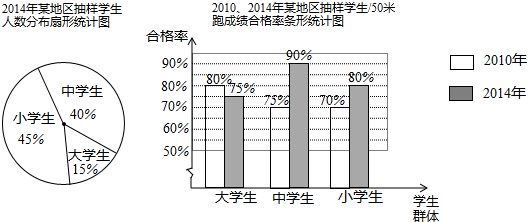
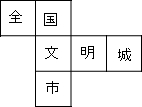 在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )
在市委、市府的领导下,全市人民齐心协力,将广安成功地创建为“全国文明城市”,为此小红特制了一个正方体玩具,其展开图如图所示,原正方体中与“文”字所在的面相对的面上标的字应是( )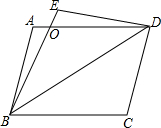 在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.
在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.


