题目内容
18.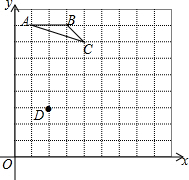 如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).(1)若D(2,3),请在网格图中画一个格点△DEF,使△DEF∽△ABC,且相似比为2:1;
(2)求△ABC中AC边上的高;
(3)若△ABC外接圆的圆心为P,则点P的坐标为(2,6).
分析 (1)利用相似比为2:1,将三角形各边扩大2倍,进而得出对应点位置即可得出答案;
(2)利用三角形面积求法得出答案;
(3)利用三角形外接圆的作法得出答案.
解答  解:(1)如图所示:△DEF即为所求;
解:(1)如图所示:△DEF即为所求;
(2)设AC边上的高为:x,
由题意可得:$\frac{1}{2}$×1×2=$\frac{1}{2}$×x×$\sqrt{10}$,
解得:x=$\frac{\sqrt{10}}{5}$;
(3)如图所示:点P(2,6)即为所求.
故答案为:(2,6).
点评 此题主要考查了相似变换以及三角形外接圆的作法,得出对应点位置是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
9.解方程(x-2)2=3(x-2)的适当方法是( )
| A. | 直接开平方法 | B. | 配方法 | C. | 公式法 | D. | 因式分解法 |
7.一个等腰三角形的两边长分别是2和4,则它的周长为( )
| A. | 8或10 | B. | 8 | C. | 10 | D. | 6或12 |
8.已知方程(k+2)x|k|-1-4x+k=0是关于x的一元一次方程,则k的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 以上都不对 |
 如图,在长为33米宽为20米的矩形空地上修建同样宽的道路(阴影部分),余下的部分为草坪,要使草坪的面积为510平方米,则道路的宽为( )
如图,在长为33米宽为20米的矩形空地上修建同样宽的道路(阴影部分),余下的部分为草坪,要使草坪的面积为510平方米,则道路的宽为( )